FiniteFieldEmbedding[ff1,ff2]
gives an embedding of the finite field ff1 in the finite field ff2.
FiniteFieldEmbedding[e1e2]
represents the embedding of the ambient field of e1 in the ambient field of e2, which maps e1 to e2.


FiniteFieldEmbedding
FiniteFieldEmbedding[ff1,ff2]
gives an embedding of the finite field ff1 in the finite field ff2.
FiniteFieldEmbedding[e1e2]
represents the embedding of the ambient field of e1 in the ambient field of e2, which maps e1 to e2.
Details

- Finite field embeddings are also known as Galois field embeddings or finite field monomorphisms.
- Finite field embeddings are typically used to identify one finite field with a subfield of another.
- If ℰ=FiniteFieldEmbedding[e1e2], where e1∈ff1 and e2∈ff2, then
 maps ff1 into ff2,
maps ff1 into ff2, 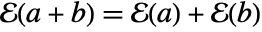 , and
, and  for all
for all 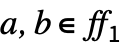 .
. - A finite field ff1 can be embedded in ff2 if it has the same characteristic as ff2 and its extension degree divides that of ff2.
- Finite field elements e1∈ff1 and e2∈ff2 define a field embedding of ff1 in ff2 iff they have the same MinimalPolynomial and e1 generates ff1. The latter condition is satisfied iff the degree of the minimal polynomial of e1 is equal to the extension degree of ff1 over
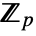 .
. - For an embedding ℰ=FiniteFieldEmbedding[e1e2], ℰ["Projection"] represents a linear mapping
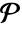 from the ambient field ff2 of e2 onto the ambient field ff1 of e1, treated as vector spaces over
from the ambient field ff2 of e2 onto the ambient field ff1 of e1, treated as vector spaces over  , such that
, such that  for all
for all 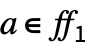 .
.
Examples
open all close allBasic Examples (1)
Scope (3)
Represent finite fields ![]() and
and ![]() with characteristic
with characteristic ![]() and extension degrees
and extension degrees ![]() and
and ![]() :
:
A field embedding preserves addition and multiplication:
ℰ["Projection"] is a ![]() -linear mapping but does not preserve multiplication:
-linear mapping but does not preserve multiplication:
The composition of ℰ["Projection"] with ![]() is the identity on
is the identity on ![]() :
:
The reverse composition is not the identity on ![]() :
:
Specify a field embedding by manually picking a generator and its value:
a generates ![]() if the degree of its minimal polynomial equals the extension degree of
if the degree of its minimal polynomial equals the extension degree of ![]() :
:
Represent the embedding of ![]() in
in ![]() that maps a to b:
that maps a to b:
For the embedding to exist, both fields need to have the same characteristic:
The extension degree of the first field needs to divide the extension degree of the second field:
Applications (1)
Factor a polynomial in an algebraic extension of a finite field:
Embed ![]() in a finite field with
in a finite field with ![]() elements:
elements:
Use the Extension option to combine the last two steps:
Properties & Relations (4)
A field embedding preserves addition and multiplication:
ℰ["Projection"] is a ![]() -linear mapping but does not preserve multiplication:
-linear mapping but does not preserve multiplication:
The composition of ℰ["Projection"] with ![]() is the identity on
is the identity on ![]() :
:
The reverse composition is not the identity on ![]() :
:
All finite field automorphisms are functional powers of the Frobenius automorphism:
Here aut[a]==FrobeniusAutomorphism[a,4]:
An embedding allows identifying ![]() with a subfield of
with a subfield of ![]() :
:
Use FiniteFieldElementTrace to compute ![]() :
:
Use FiniteFieldElementNorm to compute ![]() :
:
Use MinimalPolynomial to find the minimal polynomial of an element of ![]() over
over ![]() :
:
Use Composition to compose finite field embeddings:
Related Guides
History
Text
Wolfram Research (2023), FiniteFieldEmbedding, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.
CMS
Wolfram Language. 2023. "FiniteFieldEmbedding." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html.
APA
Wolfram Language. (2023). FiniteFieldEmbedding. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html
BibTeX
@misc{reference.wolfram_2025_finitefieldembedding, author="Wolfram Research", title="{FiniteFieldEmbedding}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finitefieldembedding, organization={Wolfram Research}, title={FiniteFieldEmbedding}, year={2023}, url={https://reference.wolfram.com/language/ref/FiniteFieldEmbedding.html}, note=[Accessed: 24-February-2026]}