FluidFlowPDEComponent
FluidFlowPDEComponent[vars,pars]
変数 vars,パラメータ pars のフローPDE(偏微分方程式)項を与える.
詳細




- FluidFlowPDEComponentは,粘性流体の流れを,適用された力と制約条件に従ってモデル化する.
- FluidFlowPDEComponentは,微分方程式の一部として使われる微分演算子の和を返す.
- FluidFlowPDEComponentは,定常,時間依存,パラメトリックの解析のためのPDE成分を作成する.
- FluidFlowPDEComponentは,流体の流れ現象を,従属変数としての速度
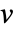 ,
,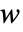 ,
,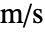 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/6.png) ]),独立変数
]),独立変数 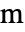 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/8.png) ]),時間変数
]),時間変数 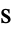 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/10.png) ])でモデル化する.
])でモデル化する. - FluidFlowPDEComponentは,2Dおよび3Dの空間次元のPDE項を作成する.
- 定常変数 vars は vars={{u[x1,…,xn],v[x1,…,xn],…,p[x1,…,xn]},{x1,…,xn}}である.
- 時間依存変数または固有モード変数の vars は vars={{u[t,x1,…,xn],v[t,x1,…,xn],…,p[x1,…,xn]},t,{x1,…,xn}}である.
- FluidFlowPDEComponentが生成する異なる解析タイプのための方程式は vars の形式に依存する.
- FluidFlowPDEComponentは,連続方程式と組み合されたベクトル値のナビエ・ストークス(Navier–Stokes)方程式系を作成する.
- 体積密度
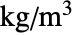 [
[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/12.png) ],流速
],流速 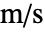 [
[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/14.png) ],時間
],時間 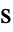 [
[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/16.png) ],粘性応力テンソル
],粘性応力テンソル 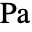 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/18.png) ],圧力
],圧力 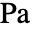 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/20.png) ],恒等
],恒等 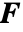 ,本体負荷
,本体負荷 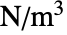 [
[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/23.png) ] のベクトル行列流体動力学PDE FluidFlowPDEComponentの時間依存平衡方程式は,ナビエ・ストークス方程式と連続方程式に基づく.
] のベクトル行列流体動力学PDE FluidFlowPDEComponentの時間依存平衡方程式は,ナビエ・ストークス方程式と連続方程式に基づく. - 可縮形式では,粘性応力テンソル
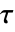 は以下で与えられる.
は以下で与えられる. - ここで,
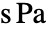 [
[![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/28.png) ]は動粘性係数であり,微小変形歪み速度測定値
]は動粘性係数であり,微小変形歪み速度測定値 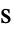 [1/
[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/30.png) ]は以下で与えられる.
]は以下で与えられる. - FluidFlowPDEComponentは,可縮または非可縮の流体流れのPDEモデルを,体積密度
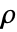 の値の性質に応じて作成する.
の値の性質に応じて作成する. - 可縮流体動力学モデルは以下で与えられる.
- 質量密度
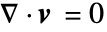 の値が一定のとき,質量連続方程式は体積連続方程式
の値が一定のとき,質量連続方程式は体積連続方程式 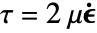 に簡約され,それにともなって粘性応力テンソルは
に簡約され,それにともなって粘性応力テンソルは 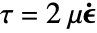 に簡約される.
に簡約される. - 非可縮流体動力学モデルは以下で与えられる.
- 定常平衡方程式は
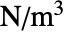 を持つ.
を持つ. - ナビエ・ストークスモデル項は力密度(単位:[
![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/39.png) ])である.
])である. - 質量連続方程式モデル項の単位は力密度(単位:[
![TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/40.png) ])および体積連続(単位:[1/
])および体積連続(単位:[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/41.png) ])である.
])である. - フローは,
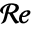 が典型である.
が典型である.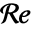 はレイノルズ(Reynolds)数である.
はレイノルズ(Reynolds)数である. - レイノルズ数
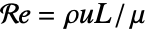 は
は 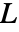 と定義される.ここで,
と定義される.ここで,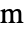 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/47.png) ]は代表的長さであり,
]は代表的長さであり,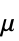 は流速である.
は流速である. - 次は,使用可能なパラメータ pars である.
-
パラメータ デフォルト シンボル "DynamicViscosity" - 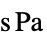 ,動粘性係数(単位:[
,動粘性係数(単位:[![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/50.png) ])
])
"FluidLoad" 0 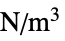 ,体積力密度(単位:[
,体積力密度(単位:[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/52.png) )
)
"FluidDynamicsMaterialModel" "Newtonian" なし "MassDensity" - 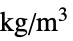 ,密度(単位:[
,密度(単位:[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.ja/54.png) ])
])
"Material" - なし "ModelForm" "Conservative" なし "ReynoldsNumber" - 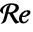
- "Material"が指定されると,材料定数は材料データから抽出される.それ以外の場合は,関連する材料パラメータを指定する必要がある.
- 材料パラメータの代りにレイノルズ数
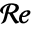 を指定することもできる.
を指定することもできる. - デフォルトの材料モデルはニュートン流体モデルである.
- パラメータ pars で"FluidDynamicsMaterialModel"キーを指定することで代替材料モデルが指定できる.
- 次の非ニュートン材料モデルも使うことができる.
-
材料モデル名 "PowerLaw" "Carreau" "Bingham-Papanastasiou" "Herschel-Bulkley-Papanastasiou" - 可縮の非ニュートン流体モデルについての粘性応力テンソル
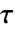 は,以下のように定義される.
は,以下のように定義される. - 見かけ粘度
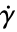 はせん断率
はせん断率 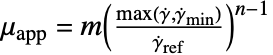 の関数である.
の関数である. - "ModelName"のモデルについての追加的な材料モデルに特有のパラメータは,"FluidDynamicsMaterialModel"-><"ModelName"-><...>>で指定できる.
- 汎用モデルの"PowerLaw"モデル,汎用モデルは
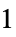 を実装する.
を実装する. - "PowerLaw"モデルには,次のパラメータを与えることができる.
-
パラメータ デフォルト シンボル "PowerLawExponent" 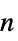
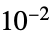 ,指数
,指数
"MinimalShearRate" 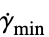
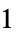 ,最小せん断率
,最小せん断率"ReferenceShearRate" 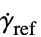
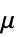 ,基準せん断率
,基準せん断率"PowerLawViscosity" 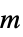
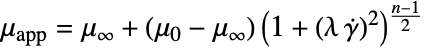 ,ベキ乗則粘度
,ベキ乗則粘度 - 高分子流あるいは血流に有用な一般化された"Carreou"モデルは
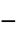 を実装する.
を実装する. - "Carreau"モデルには,次のパラメータを与えることができる.
-
パラメータ デフォルト シンボル "PowerLawExponent" 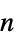
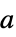 ,指数
,指数
"TransitionExponent" 2 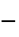 ,指数
,指数"InfiniteShearRateViscosity" 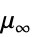
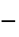 ,無限せん断率における粘度
,無限せん断率における粘度"Lambda" 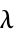
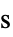 ,緩和時間(単位:[
,緩和時間(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.ja/79.png) ])
])"ZeroShearRateViscosity" 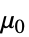
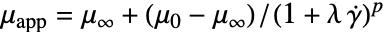 ,せん断率0における粘度
,せん断率0における粘度 - "Carreau"モデルも
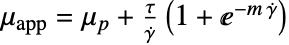 のCrossモデルに使うことができる.ただし,
のCrossモデルに使うことができる.ただし,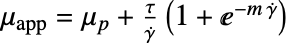 である.
である. - 粘塑性材料に有用な"Bingham-Papanastasiou"モデルは
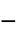 を実装する.
を実装する. - "Bingham-Papanastasiou"モデルには,次のパラメータを与えることができる.
-
パラメータ デフォルト シンボル "PlasticViscosity" 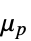
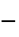 ,塑性粘度
,塑性粘度
"YieldStress" 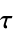
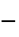 ,降伏応力
,降伏応力"ShearRateFactor" 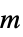
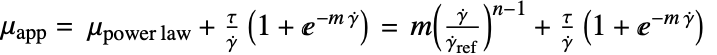 ,せん断率係数
,せん断率係数 - "PowerLaw"モデルと"Bingham-Papanastasiou"の混合である"Herschel-Bulkley-Papanastasiou"モデルは
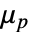 を実装する.このモデルは,ベキ乗則を用いてBingham–Papanastasiouモデルの塑性粘度
を実装する.このモデルは,ベキ乗則を用いてBingham–Papanastasiouモデルの塑性粘度 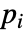 を計算する.両方のモデルのパラメータを設定することができる.
を計算する.両方のモデルのパラメータを設定することができる. - カスタムの見かけ粘度関数 fun は,"FluidDynamicsMaterialModel"-><"Custom"-><"ApparentViscosityFunction"->fun>>として設定できる.
- カスタムの見かけ粘度関数 fun の関数シグネチャはfun[name_,vars_,pars_,data__]である.
- カスタムの粘性応力テンソル関数 fun は,"FluidDynamicsMaterialModel"->funと指定することができる.
- スタムの粘性応力テンソル関数 fun の関数シグネチャはfun[vars_,pars_,data__]である.
- 非等温流はBoussinesq近似を使ってモデル化できる.
- FluidFlowPDEComponentは"SIBase"単位を用いる.形状はPDEと同じ単位でなければならない.
- FluidFlowPDEComponentが連想 pars によって…,keypi…,pivi,…]として指定されるパラメータ
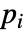 に依存するなら,パラメータ
に依存するなら,パラメータ 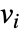 は
は 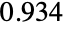 で置換される.
で置換される.
例題
すべて開くすべて閉じる例 (4)
スコープ (8)
特定の材料についてのフローPDEモデルをActivateする:
二次元,動粘性係数 ![]() ,質量密度
,質量密度 ![]() の記号定常流体動力学PDEを指定する:
の記号定常流体動力学PDEを指定する:
三次元,動粘性係数 ![]() ,質量密度
,質量密度 ![]() の記号定常流体動力学PEDを指定する:
の記号定常流体動力学PEDを指定する:
二次元,動粘性係数 ![]() ,質量密度
,質量密度 ![]() の記号時間依存流体動力学PDEを指定する:
の記号時間依存流体動力学PDEを指定する:
アプリケーション (3)
非ニュートン流動 (1)
テキスト
Wolfram Research (2024), FluidFlowPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html (2024年に更新).
CMS
Wolfram Language. 2024. "FluidFlowPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html.
APA
Wolfram Language. (2024). FluidFlowPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html