FluidFlowPDEComponent[vars,pars]
yields a flow PDE term with variables vars and parameters pars.


FluidFlowPDEComponent
FluidFlowPDEComponent[vars,pars]
yields a flow PDE term with variables vars and parameters pars.
Details








- FluidFlowPDEComponent models flow of viscous fluids subject to applied forces and constraints.
- FluidFlowPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- FluidFlowPDEComponent models fluid flow phenomena with velocities
 ,
,  and
and  in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/5.png) ] as dependent variables,
] as dependent variables, 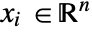 as independent variables in units of [
as independent variables in units of [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.en/7.png) ] and time variable
] and time variable 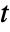 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.en/9.png) ].
]. - FluidFlowPDEComponent creates PDE components for stationary, time-dependent, parametric analysis.
- FluidFlowPDEComponent creates PDE components in two and three space dimensions.
- Stationary variables vars are vars={{u[x1,…,xn],v[x1,…,xn],…,p[x1,…,xn]},{x1,…,xn}}.
- Time-dependent or eigenmode variables vars are vars={{u[t,x1,…,xn],v[t,x1,…,xn],…,p[x1,…,xn]},t,{x1,…,xn}}.
- The equations for different analysis types that FluidFlowPDEComponent generates depend on the form of vars.
- FluidFlowPDEComponent creates a system of equations with the vector-valued Navier–Stokes equation combined with the continuity equation.
- The time-dependent equilibrium equation of the fluid dynamics PDE FluidFlowPDEComponent with mass density
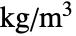 [
[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/12.png) ], fluid velocity
], fluid velocity 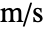 [
[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/14.png) ], time
], time 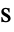 [
[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.en/16.png) ], viscous stress tensor
], viscous stress tensor 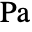 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.en/18.png) ], pressure
], pressure 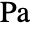 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.en/20.png) ], identity matrix
], identity matrix 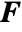 and body load vectors
and body load vectors 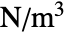 [
[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/23.png) ] is based on the Navier–Stokes equation and the continuity equation:
] is based on the Navier–Stokes equation and the continuity equation: - In compressible form, the viscous stress tensor
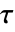 is given as:
is given as: - Here
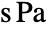 [
[![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.en/28.png) ] is the dynamic viscosity, and infinitesimal, small deformation strain rate measure
] is the dynamic viscosity, and infinitesimal, small deformation strain rate measure 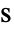 [1/
[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.en/30.png) ] is given as:
] is given as: - FluidFlowPDEComponent creates a PDE model for compressible or incompressible fluid flow, depending on the nature of the values of the mass density
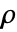 .
. - The compressible fluid dynamics model is given as:
- For constant values of the mass density
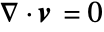 , the mass continuity equation simplifies to a volumetric continuity equation
, the mass continuity equation simplifies to a volumetric continuity equation 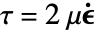 , and with that, the viscous stress tensor simplifies to
, and with that, the viscous stress tensor simplifies to 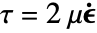 .
. - The incompressible fluid dynamics model is given as:
- The stationary equilibrium equations have
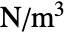 .
. - The units of the Navier–Stokes model terms are a force density in [
![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/39.png) ].
]. - The units of the mass continuity equation model terms are a force density in [
![TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/40.png) ], and for the volumetric continuity [1/
], and for the volumetric continuity [1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.en/41.png) ].
]. - Laminar flow is typical for
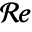 , where
, where 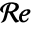 is the Reynolds number.
is the Reynolds number. - The Reynolds number
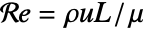 is defined as
is defined as 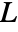 , where
, where 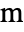 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.en/47.png) ] is a characteristic length and
] is a characteristic length and 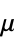 the flow velocity.
the flow velocity. - The following parameters pars can be given:
-
parameter default symbol "DynamicViscosity" - 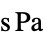 , dynamic viscosity [
, dynamic viscosity [![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.en/50.png) ]
]
"FluidLoad" 0 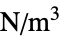 , body force density [
, body force density [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/52.png) ]
]
"FluidDynamicsMaterialModel" "Newtonian" none "MassDensity" - 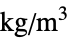 , density in [
, density in [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.en/54.png) ]
]
"Material" - none "ModelForm" "Conservative" none "RegionSymmetry" None - "ReynoldsNumber" - 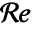
- If a "Material" is specified, the material constants are extracted from the material data; otherwise, relevant material parameters need to be specified.
- Instead of material parameters, a Reynolds number
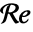 can be specified:
can be specified: - "RegionSymmetry"->"Axisymmetric" uses a truncated cylindrical coordinate system and assumes
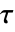 in the
in the 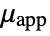 direction and pressure
direction and pressure 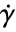 and velocity components
and velocity components 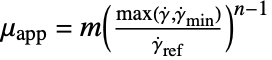 and
and 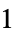 independent of
independent of 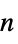 .
. - The axis of symmetry is the
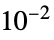 axis.
axis. - The default material model is a Newtonian flow model.
- Alternate material models can be specified by setting the "FluidDynamicsMaterialModel" key in parameters pars.
- The following non-Newtonian material models are available:
-
material model name "PowerLaw" "Carreau" "Bingham-Papanastasiou" "Herschel-Bulkley-Papanastasiou" - For compressible non-Newtonian fluids, the viscous stress tensor
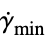 is defined as:
is defined as: - The apparent viscosity
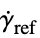 is a function of the shear rate
is a function of the shear rate 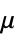 .
. - Additional material model-specific parameters for a model with "ModelName" can be specified through "FluidDynamicsMaterialModel"-><|"ModelName"-><|...|>|>.
- The "PowerLaw" model, a general-purpose model, implements
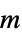 .
. - The following parameters can be given for the "PowerLaw" model:
-
parameter default symbol "PowerLawExponent" 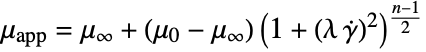
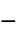 , exponent
, exponent
"MinimalShearRate" 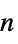
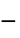 , minimal shear rate
, minimal shear rate"ReferenceShearRate" 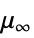
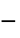 , reference shear rate
, reference shear rate"PowerLawViscosity" 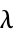
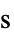 , power law viscosity
, power law viscosity - The generalized "Carreau" model, useful for polymer or blood flow, implements
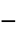 .
. - The following parameters can be given for the "Carreau" model:
-
parameter default symbol "PowerLawExponent" 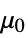
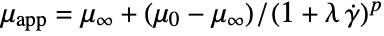 , exponent
, exponent
"TransitionExponent" 2 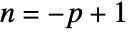 , exponent
, exponent"InfiniteShearRateViscosity" 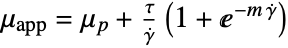
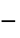 , viscosity at inifinite shear rate
, viscosity at inifinite shear rate"Lambda" 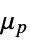
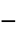 , relaxation time [
, relaxation time [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.en/86.png) ]
]"ZeroShearRateViscosity" 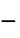
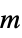 , viscosity at zero shear rate
, viscosity at zero shear rate - The "Carreau" model can also be used for a Cross model where
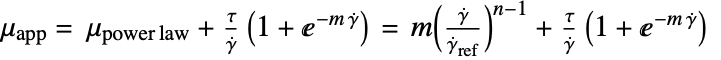 with
with 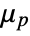 .
. - The "Bingham-Papanastasiou" model, useful for viscoplastic material, implements
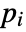 .
. - The following parameters can be given for the "Bingham-Papanastasiou" model:
-
parameter default symbol "PlasticViscosity" 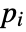
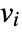 , plastic viscosity
, plastic viscosity
"YieldStress" 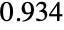
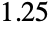 , yield stress
, yield stress"ShearRateFactor" 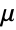
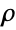 , shear rate factor
, shear rate factor - The "Herschel-Bulkley-Papanastasiou" model, a mixture of a "PowerLaw" and "Bingham-Papanastasiou" model, implements
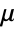 . The model uses a power law to compute the plastic viscosity
. The model uses a power law to compute the plastic viscosity 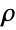 of the Bingham–Papanastasiou model, and parameters for both models can be set.
of the Bingham–Papanastasiou model, and parameters for both models can be set. - A custom apparent viscosity function fun can be specified as "FluidDynamicsMaterialModel"-><|"Custom"-><|"ApparentViscosityFunction"->fun|>|>.
- A custom apparent viscosity function fun has a function signature fun[name_,vars_,pars_,data__].
- Custom viscous stress tensor functions fun can be specified as "FluidDynamicsMaterialModel"->fun.
- A custom viscous stress tensor function fun has a function signature fun[vars_,pars_,data__].
- Non-isothermal flow can be modeled through the Boussinesq approximation.
- FluidFlowPDEComponent uses "SIBase" units. The geometry has to be in the same units as the PDE.
- If the FluidFlowPDEComponent depends on parameters
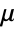 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 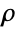 are replaced with
are replaced with 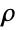 .
.
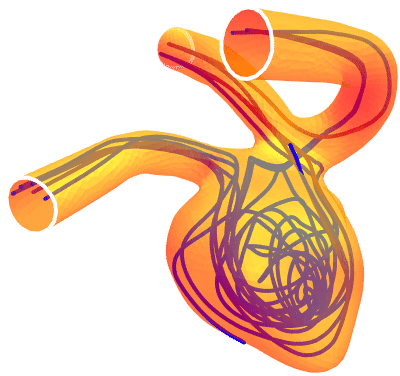
Examples
open all close allBasic Examples (4)
Scope (10)
2D (4)
Define a flow PDE model for a specific material:
Specify a flow PDE with a dynamic viscosity of ![]() and a mass density of
and a mass density of ![]() :
:
Activate a flow PDE model for a specific material:
Specify a symbolic stationary fluid dynamics PDE in two dimensions with a dynamic viscosity of ![]() and a mass density of
and a mass density of ![]() :
:
2D Axisymmetric (1)
3D (1)
Time Dependent (3)
Applications (5)
Stationary Analysis (1)
Non-Newtonian Flow (1)
Compute the fluid flow of a non-Newtonian fluid in an opening channel by using the power law fluid flow model.
Set up variables, flow parameters and the non-Newtonian power law for parameters for the exponent and power law viscosity:
Solve the PDE with an inflow profile given as {1/2,0} and with the outflow pressure set to 0. The walls are set up as no-slip walls:
Visualize the velocity in the region:
Plot the flow profile from the middle of the channel to the top scaled to 1:
Time-Dependent Analysis (1)
Solve a time-dependent driven cavity problem.
Create and visualize an auxiliary function to ramp up the flow speed on top of the box:
Set up the boundary conditions:
Set up the initial conditions:
Monitor the solution process and measure the time it takes to solve the PDE:
Visualize rasterized frames of the velocity field for various times:
Axisymmetric Flow (2)
Compute the fluid flow in a narrowing cylindrical pipe driven by a parabolic inflow. Set up the axisymmetric domain:
Set up the boundary conditions:
Visualize the velocity of the solution:
Plot the pressure in 3D for part of the pipe:
Compute the velocity profile for time-dependent axisymmetric flow driven by a pressure gradient. Set up the domain:
Set up the boundary conditions with a prescribed pressure gradient:
Solve the equations and measure the time it takes:
Tech Notes
Related Guides
Text
Wolfram Research (2024), FluidFlowPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html (updated 2025).
CMS
Wolfram Language. 2024. "FluidFlowPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html.
APA
Wolfram Language. (2024). FluidFlowPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_fluidflowpdecomponent, author="Wolfram Research", title="{FluidFlowPDEComponent}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html}", note=[Accessed: 24-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_fluidflowpdecomponent, organization={Wolfram Research}, title={FluidFlowPDEComponent}, year={2025}, url={https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html}, note=[Accessed: 24-January-2026]}