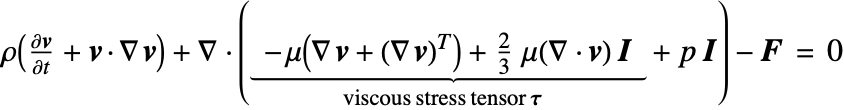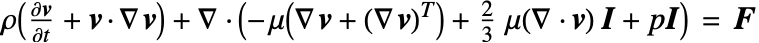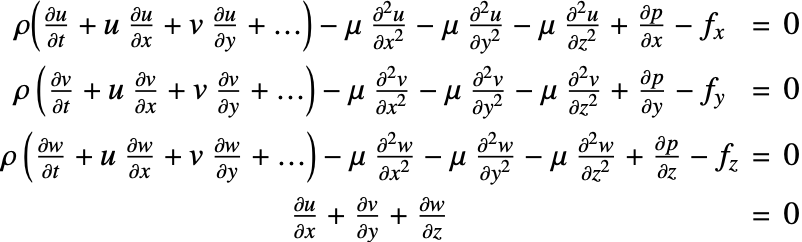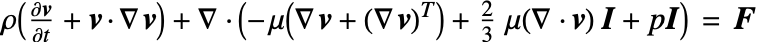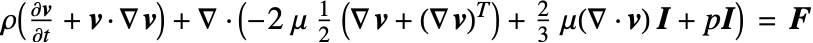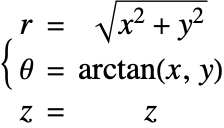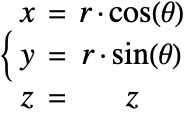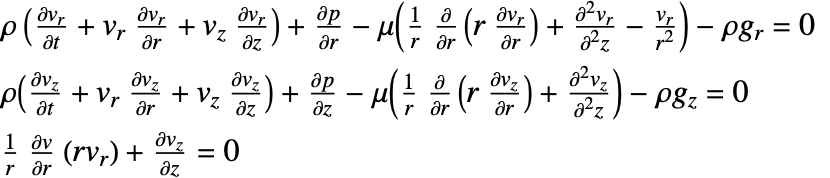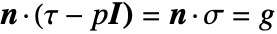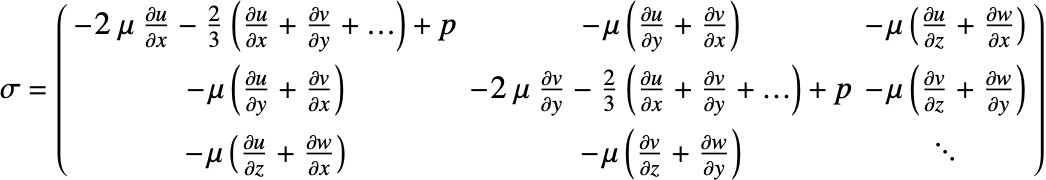Laminar Flow
Introduction
The analysis and behaviour of fluids is of fundamental importance in science and engineering. This monograph gives an introduction to modeling fluids with partial differential equations. Equations and boundary conditions that are relevant for performing fluid mechanics analysis are derived and explained.
Fluids are substances in gaseous or liquid phase, like air or water, respectively. The term 'fluid' comprises both liquids and gases. The opposite of fluids are solids and the distinguishing attribute is that fluids can not withstand shear forces when at rest.
Typically we differentiate between different fluid flow regimes:
This monograph focuses on laminar flow.
Modeling fluids with partial differential equations (PDEs) is not the only way to model fluids. Other techniques include setting up ordinary differential equations (ODEs). This approach is followed by the Wolfram System Modeler. Roughly speaking the system modeler approach is more suitable for large systems of flows interacting, like flow though pipes, while the partial differential equation approach is more suitable for a fine grained analysis of a specific fluid flow behaviour. In some cases it is beneficial to use a combination of the two approaches.
The approach taken here is that in an introductory section a single fluid flow example, a driven cavity example, is used to introduce various fluid flow analysis types and the functionality available. This will be followed by a more theoretical explanation of the underlying ideas and concepts. The theoretical background is much easier to understand once an intuition for the various analysis types exist. After that the available boundary conditions are discussed.
The goal of a fluid flow analysis is to find the vector valued fluid flow velocities and the scalar pressure field of a fluid under constraints. The analysis and interpretation of the fluid behaviour is useful to create a better quality engineering design of the flow behaviour in question. For example, through some parts of an object there might not be sufficient flow. These areas can then be identified and improved upon.
A fluid flow analysis is typically done in stages. First, for the body in which the fluid flows, a geometric model needs to be created. The geometric model is typically created within a computer aided design (CAD) process. CAD models can either be imported or created in product. To import geometries common file formats like DXF, STL or STEP are supported. These geometries can be imported with Import. The alternative is to create the geometrical models in product with, for example, by using OpenCascadeLink. Once the geometric model is made available, some thought needs to be put into what what type of analysis is to be performed. Currently supported analysis types are static and time dependent fluid flow analysis. The next step is the setup of boundary conditions and constraints. Material properties of the fluid in question further specify the PDE model. Once the PDE model is fully specified, the subsequent finite element method will then compute the desired quantities under investigation. These quantities are then post processed. Either by visualizing them or some derived quantities are computed. This notebook shows the necessary steps for everything except the CAD model generation.
The modeling process as such results in a system of partial differential equations (PDEs) that can be solved with NDSolve and ParametricNDSolve.
Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high quality graphics remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Many of the animations of the simulation results shown in this notebook are generated with a call to Rasterize. This is to reduce the disk space the this notebook requires. The downside is that the visual quality of the animations will not be as crisp as without it. To obtain high quality graphics remove or comment out the call to Rasterize.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Overview Example and Analysis Types
We start with an overview example, where we focus on the workflow more than the actual equations and theory. For this example we consider the flow of glycerol in a narrowing tube.
Creating a fluid flow model always comprises the same steps:
The dependent velocity variables 
, 
represent the displacement in the 
, and 
-directions, respectively. 
is the pressure.
Here we made use of chemical entity. Alternatively, we could specify material properties.
The inflow velocity in the 
-direction is prescribed through boundary conditions. This is done by specifying an inflow profile for the 
dependent variable on the left-hand side of the region. On the bottom and upper part of the region, a wall boundary condition is specified. This is done by setting both the 
and 
components on those parts to 0. An outflow condition is set on the right-hand side of the domain. Here the pressure 
is arbitrarily set to 0. In general, each dependent variable should either have a Dirichlet condition or a Robin-type Neumann specified. A pure Neumann value like Neumann 0 is not sufficient. In that case, the solution to the equation can only be correct up to a constant.
A stable solution can be found if the velocities are interpolated with a higher order than the pressure. NDSolve allows an interpolation order for each dependent variable to be specified. Most of the time specifying the "InterpolationOrder" is not necessary, but this is a standard procedure when using the finite element method for fluid flow and this is how it can be done in the Wolfram Language. This setup corresponds to what is called P2P1- or Q2Q1-type elements, which are also known as Taylor–Hood elements. Leaving out the "InterpolationOrder" will result in using a second-order interpolation for all variables, which can lead to instabilities.
In many cases there is no need to generate a mesh, passing the geometry to the solver is sufficient.
This gives an overview of the workflow. The next sections describe the steps in more detail.
Stationary Analysis
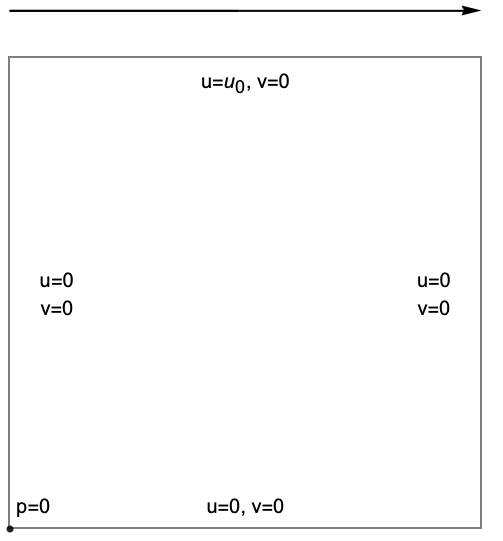
In this example, the driven cavity example, we investigate a classic benchmark in fluid dynamics [6]. Here a rectangular region is filled with a fluid. On the top we have a mechanism that drives the fluid with a fixed flow velocity in the positive 
-direction, much like a conveyor belt would. The remaining sides are walls and have a no-slip condition. No-slip means that the velocity at the wall boundary is 0 in both the 
- and 
-direction. In the lower left corner we have a reference pressure condition.
In a rectangular region filled with a fluid, the top is driven by a velocity 
in the 
- direction. All other edges are walls, where a no-slip, 
, boundary condition is set.
This driven cavity will be modeled as a time independent, a stationary, model. We set up the dependent velocity variables 
and 
and the dependent pressure variable 
. The independent variables are the spatial variables 
and 
.
Standard texts present this example with various Reynolds numbers 
. With everything else remaining the same the flow pattern changes, depending only on the values of the Reynolds number 
.
A reference pressure point should be applied in a 'calm' area, or in other words far away from the interesting behaviour.
The solution returned constrains the 
velocity profile, which is the velocity profile in the 
direction, the 
velocity profile which is the velocity profile in the 
direction and a pressure distribution 
. There are various ways to visualize the solution.
The "InterpolationOrder" method option given to NDSolve specifies that the both velocities are interpolated with second order and that the pressure is interpolated with first order. The "InterpolationOrder" option specification is equivalent, to what is known in the finite element world, as a Taylor-Hood element and it helps stabilize the solution. Unfortunately, there is no known way to automatically set this option for specific PDEs and it is recommenced that the option is set for fluid flow PDEs that are based on the Navier-Stokes equation, like the FluidFlowPDEComponent.
Post Processing
The computed pressure is a scalar field and as such can be visualized like any other scalar field. Contour or density plots are a good way to visualize these.
The velocity field is a vector valued field. Here, vector -, stream - or line integral convolution plots are a good choice for visualization.
In 2 dimensions a vorticity plot can also provide useful information.
Parametric Analysis
As a next step, we would like to compare the flow field for various Reynolds numbers. We would like to use the Reynolds number as a parameter. ParametricNDSolve works just like NDSolve, with the addition that parameters can be specified. ParametricNDSolve then returns a function, then when feed numerical values for the parameters with compute the numerical solution.
In the previous example, where we used NDSolve, we stored the solution in a list of the form {uVel,vVel,pressure}. Now, we store the solution of all simulation runs in the variable solutions. Each entry in the solutions vector now contains an interpolation function for the 
-field, the 
-field and the pressure 
.
Too large a Reynolds number will eventually prohibit convergence of the nonlinear PDE as the PDE then becomes too strongly nonlinear. A failure in convergence is typically announced by a message from FindRoot as FindRoot is the function that eventually solves the nonlinear equations within NDSolve. Not all hope is lost then, however. There are various measures that can be taken to extend the range in which a model converges.
There are various ways to circumvent the loss of convergence, which are discussed in the section Convergence of Fluid Flow Models. Here we take a closer look at the mesh used for the analysis. In the above example a mesh was generated automatically. One option is to make use of a mesh that is more appropriate for the problem at hand. The specifics of what 'more appropriate' means depend on the problem at hand. For this example, note that the gradient of the 
- and 
-velocity field are largest at the top and at the right wall.
The mesh we generate should reflect the steep gradients by having a finer resolution at steep gradients. Seen that the flow gradient is higher at the walls, a possible way to improve on that is to make use of a graded mesh. This can be done with the function ToGradedMesh. This allows for more refinement at the boundary while not increasing the overall number of elements too much. Other refinement options like using a MeshRefinementFunction are also possible. More information about the mesh generation process can be found in the ElementMesh generation tutorial.
With the graded mesh, we have reduced the overall number of elements and at the same time increased the element density near the walls.
See this note about improving the visual quality of the animation.
Since the driven cavity is a common fluid dynamics benchmark problem [6] literature data exists that can be used to compare numerical simulations.
The solution matches the literature values.
For computing even higher Reynolds numbers of the driven cavity example see the section Convergence of Fluid Flow Models.
Time Dependent Analysis
As a next workflow example, we solve the time dependent driven cavity example. Now, the fluid is initially at rest and the driving mechanism will ramp up with time. Everything else remains the same.
For the inflow boundary condition to be consistent with initial conditions a helper function, that smoothly ramps up the inflow over time, is created.
It is possible to monitor the time integration.
See this note about improving the visual quality of the animation.
Equations
When planing a fluid flow simulation a first step is to classify what flow regime is to be expected. For this we use characteristic numbers that capture various aspects of flow behaviour. One characterization is done through the Reynolds number 
. The Reynolds number is the ratio of internal force in the fluid to the fluids viscosity.
Here 
[
]is the dynamic viscosity, 
[
]is the density, 
[
] is a typical flow velocity and 
[
] is a characteristic length. The Reynolds number gives us an approximate indication of what type of flow we can expect.
Flow with 
are in the creeping flow regime. For flows where the Reynolds number is larger then, say, 
turbulence can appear. At what particular Reynolds number a flow transitions from laminar to turbulent depends on the specifics of that particular flow. For example, in tubes a value of 
can induce turbulence flow. Contrary to that flow along a flat plate will become turbulent only for 
.
Typically we differentiate between different fluid flow regimes:
Honey, compared to water, is a viscous fluid. The higher the viscosity of a fluid the more likely it will show laminar flow behaviour. Gases, on the other hand have very low viscosity and the Reynolds number approaches infinity. Gases as also called inviscid fluids.
Laminar flow is described by a set of vector valued equations called the Navier-Stokes equation. A wide range of fluid flow phenomena can be described with the Navier-Stokes equation, even beyond laminar flow. The Navier-Stokes equations is the overarching equation in fluid dynamics. The Navier-Stokes equation are a set of partial differential equations and exist in various forms, depending on the flow regime one is interested in.
The Navier-Stokes equation is a combination of a momentum equation and the continuity equation.
The momentum equation for a compressible fluid flow is a vector valued equation expressed with the viscous stress tensor 
in [
]:
The viscous stress tensor 
is given as:
Inserting the definition of the viscous stress tensor 
into the momentum equation gives:
Some formulations of the Navier-Stokes momentum equation contain an additional term 
called second viscosity, or volume viscosity, such that
but for most practical purposes 
is negligible and 
.
The units of the momentum equations are a force density in [
]. The conservation of momentum is essentially Newton's second law of motion for fluids. This can be seen when we slightly rearrange the equation:
The momentum equation is almost always solved together with the mass continuity equation which describes the conservation of mass:
with density 
the dependent variable and the fluid flow velocity vector 
.
The Navier-Stokes equation is only valid when the smallest geometrical feature of the domain are still much larger then then mean free path of the fluid's molecules.
The Navier-Stokes equation is for compressible, weakly compressible and incompressible flow. Weakly compressible flow means that a pressure dependence of density can be neglected and is evaluated at a reference pressure.
For constant values of the mass density 
the mass continuity equation simplifies to a volumetric continuity equation 
and with that the viscous stress tensor simplifies to 
. When 
is constant, we can write 
as 
since in that case the divergence 
.
The incompressible form of the Navier-Stokes equation is:
The incompressible Navier-Stokes equation written out in component form is given as:
For a constant dynamics viscosity 
we can further simplify to:
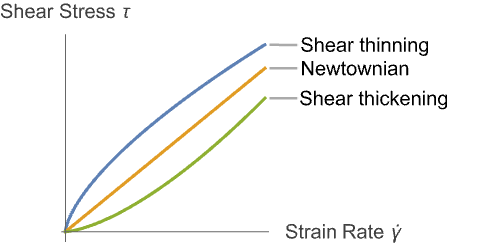
Newtonian versus non-Newtonian Flow
The viscosity of a non-Newtonian fluid changes with the applied forces. For a Newtonian fluid, such as water or honey, the viscosity does not change deepening on how much the water is stirred. For non-Newtonian fluids the amount the stirring changes the viscosity. Some materials become harder when they are stirred while others become easier to stir. In practice all gases and most liquids can be considered Newtonian. Non-Newtonian liquids are things like paint, blood, water-starch mixtures or liquid polymers.
In the following section various non-Newtonian fluid flow models are introduced. We start a derivation from the compressible Navier-Stokes equation:
Now, we can define the strain rate tensor 
in units of [1/s]:
Note, that this strain rate looks very much like the infinitesimal strain measure defined in solid mechanics. In solid mechanics the dependent variable 
is the displacement in [m] and 
defines the infinitesimal strain. In fluid dynamics the dependent variable 
is the velocity in [m/s] and 
is a strain rate tensor. The strain rate tensor is also referred to as the rate or strain tensor.
And the viscous stress tensor 
in [Pa] for a Newtonian fluid is:
This leaves us with a different formulation for the Navier-Stokes equation:
For non-Newtonian fluids the stress strain rate relation is nonlinear. This nonlinearity can be expressed in terms of an apparent viscosity 
, where the apparent viscosity is a function of the shear rate 
in [1/s]. Sometimes the apparent viscosity 
is also called the effective viscosity.
For simplicity, but without restriction to generality, we assume an incompressible non-Newtonian fluid, such that the 
term is not present and we have:
The shear rate is computed as:
where 
is the contraction and computed by
A function to compute the shear rate is implanted as follows:
ShearRate[strainRate_] :=
Sqrt[2 * TensorContract[strainRate * strainRate, {{1}, {2}}]];
The dynamic viscosity may depend on temperature and pressure and for non-Newtonian fluids the dynamic viscosity additionally depends of the shear rate.
Different non-Newtonian constitutive models are used to express the apparent viscosity 
. The following non-Newtonian fluid flow models are implemented:
For all models presented below the parameters pars need an entry for the "FluidDynamicsMaterialModel"
Power law
The power law model is a commonly used non-Newtonian fluid model.
where 
is a factor that defaults to the dynamic viscosity 
. The reference shear rate 
has a default of 1 [1/s]. The default minimal shear rate 
is set to 
[1/s]. The scalar 
is an exponent. For 
we can get a Newtonian flow and as such the power law implements a generalized Newtonian fluid model. For 
we have a shear thinning fluid, also called a pseudo-plastic fluid. Paint, blood or ketchup fall in this category. For 
we have a shear thickening fluid, also called dilatant fluids. An example for a shear thickening fluid is a mixture of water and cornstarch or quicksand.
The model given here deviates a bit from what is normally found in literature. The original model predicts an infinite viscosity as the shear rate goes to zero. In real fluids the shear rate tends to some constant value 
. This shortcoming of the original formulation is avoided be the formulation given here. A disadvantage of power law model is that it can not describe a Newtonian plateau. The Carreou model does that.
The power law is often given as an expression of the kinematic viscosity:
where 
is called the consistency index.
An illustration of shear flow versus Newtonian flow is given below.
Compare the strain rate versus shear stress for shear thickening and thinning flows with Newtonian flows.
We see that for shear thinning fluids the apparent viscosity is reduced for an increased strain rate and for a shear thickening fluid the apparent viscosity is increased for an increased strain rate.
The actual implementation of the power law model for non-Newtonian flow is given below and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["PowerLaw", vars_, pars_, data__]:=
Module[
{model, strainRate, shearRate, m, apparentViscosity, minShearRate, n, refShearRate},
model = pars["FluidDynamicsMaterialModel"]["PowerLaw"];
minShearRate = model["MinimalShearRate"];
refShearRate = model["ReferenceShearRate"];
n = model["Exponent"];
m = model["PowerLawViscosity"];
strainRate = "StrainRate" /. data;
shearRate = ShearRate[strainRate];
apparentViscosity = m * (Max[shearRate, minShearRate]/refShearRate)^(n-1);
apparentViscosity
]
The following section gives an example of a power law non-Newtonian flow.
In the given example the kinematic viscosity is specified. Since the density is given as 1 the kinematic viscosity equals the dynamic viscosity 
.
To experiment, we make the power law exponent 
and the power law factor 
symbolic parameters.
The inflow profile is given as {1/2,0} and at the outflow the pressure is set to 0. The wall as no-slip walls.
Carreou
The Carreou model also implements a generalized Newtonian flow model and is useful to model polymer flows. The Carreou model implements:
where 
is the infinite shear rate viscosity, 
is the zero shear rate viscosity. 
is a relaxation time with units [s].
For 
the Carreou model reduces to a Newtonian flow. For 
the Carreou model approaches the power law model.
The Carreou model enables the description of Newtonian plateaus for very small and very large shear rates.
The actual implementation of the Carreou model for non-Newtonian flow is given below and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["Carreou", vars_, pars_, data__]:=
Module[
{model, mu0, muInf, n, lambda, strainRate, shearRate, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Carreou"];
mu0 = model["ZeroShearRateViscosity"];
muInf = model["InfiniteShearRateViscosity"];
n = model["Exponent"];
lambda = model["Lambda"];
strainRate = "StrainRate" /. data;
shearRate = ShearRate[strainRate];
apparentViscosity = muInf + (mu0 - muInf) *
(1 + (lambda * shearRate)^2 )^((n-1)/2);
apparentViscosity
]
Cross
The cross model is an empirical model and is useful for polymer melts or polymeric solutions. The Carreou model can be used to model a cross power law:
where 
that can be specified by setting 
.
Bingham-Papanastasiou
The Bingham-Papanastasiou model is useful for viscoplastic material. The Bingham-Papanastasiou model implements:
The actual implementation of the Bingham-Papanastasiou model for non-Newtonian flow is given below and the way this model is constructed can be used as an example for constructing other non-Newtonian flow models.
ApparentViscosity["Bingham-Papanastasiou", vars_, pars_, data__]:=
Module[
{model, mup, sigma, m, strainRate, shearRate, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Bingham-Papanastasiou"];
mup = model["PlasticViscosity"];
sigma = model["YieldStress"];
m = model["ShearRateFactor"];
strainRate = "StrainRate" /. data;
shearRate = ShearRate[strainRate];
apparentViscosity = mup + sigma/shearRate * (1 - Exp[-m * shearRate]);
apparentViscosity
]
Herschel-Bulkley-Papanastasiou
The Herschel-Bulkley-Papanastasiou model implements:
The model uses a power law to compute the plastic viscosity of the Bingham-Papanastasiou model. As all parameters for the power law and Bingham-Papanastasiou model can be specified with the exception of the "PlasticViscosity" that is computed by the power law. The "MinimalShearRate" is set to -∞.
ApparentViscosity["Herschel-Bulkley-Papanastasiou", vars_, pars_, data__]:=
Module[
{model, powerLawPars, mup, binghamPapanastasiouPars, apparentViscosity},
model = pars["FluidDynamicsMaterialModel"]["Herschel-Bulkley-Papanastasiou"];
powerLawPars = pars;
powerLawPars["FluidDynamicsMaterialModel"] = <|"PowerLaw" -> model|>;
mup = ApparentViscosity["PowerLaw", vars, powerLawPars, data];
binghamPapanastasiouPars = pars;
model["PlasticViscosity"] = mup;
binghamPapanastasiouPars["FluidDynamicsMaterialModel"] =
<|"Bingham-Papanastasiou"-> model|>;
apparentViscosity = ApparentViscosity["Bingham-Papanastasiou", vars,
binghamPapanastasiouPars, data];
apparentViscosity
]
Custom apparent viscosity model
If your favorite model is not in the list given so far it can, never the less, be used by specifying a custom viscosity model.
The function myApparentViscosity has the following signature:
myApparentViscosity[_, vars_, pars_, data__]:=
Module[{},
....
]
The function myApparentViscosity should return a scalar value for the apparent viscosity. Other models given in this monograph can serve as a template for writing an apparent viscosity function.
Custom viscous stress tensor
The entire viscous stress tensor 
can be replaced by a function myViscousStressTensor
The function myViscousStressTensor has the following signature:
myViscousStressTensor[vars_, pars_, data__]:=
Module[{},
....
]
The function myViscousStressTensor should return a viscous stress tensor.
Viscoelastic flow
In viscoelastic flow the viscous stress tensor 
in [Pa] for incompressible flow is given by:
where 
is a viscoelastic stress tensor. The equations involving viscoelastic flow can quickly become numerically unstable and the usage of stabilization techniques is necessary. Since this version of NDSolve does not offer stabilization techniques, viscoelastic flow is not implemented currently.
Energy Transport - Nonisothermal Flow
Often one wants to get an understanding of how a temperature differences affect the flow of a fluid, or, how heat is transported with the fluid flow. To achieve this the Navier-Stokes equation is coupled with a heat transfer equation:
where 
is absolute temperature in [
], 
the specific heat capacity at a specific pressure in [
], 
the thermal conductivity in [
] and 
heat source densities, or, if you will energy densities, in [
]. A detailed explanation and derivation of the heat equation can be found in the Heat Transfer Monograph. Among the heat sources could be a viscous heating 
or terms the describe work done by changes in pressure. Both are often negligible but can be added if need be.
The key point is that a change in temperature induces a change in density. The volume increases and thus the weight decreases and the fluid rises: A temperature dependent buoyancy force arises.
Boussinesq Approximation
A common simplification to model the coupling of the heat and Navier-Stokes equation is the Boussinesq approximation which is based on the following assumptions [2, p.126]:
The first item allows to use the incompressible form of the continuity equation:
The momentum equation is then given as:
Note the introduction of 
, and 
is the gravitational field. The product of 
is the buoyancy contribution. As a further simplification, the Boussinesq approximation assumes a linear relation between the density 
and temperature 
:
where 
is the thermal expansion coefficient and 
and 
are reference values. In fact the equation is a first order Taylor expansion around 
. We mention in passing that the linear relation ship between 
and 
needs to be replaced with a close to quadratic relationship for special cases, like pure water at 
[4].
The Boussinesq approximation provides a coupling between the flow equations and the heat transfer model. A temperature difference is now capable to drive the fluid flow: If a flow flied is isothermal, that means 
, then the fluid will remain at rest. If, however, one wall is heated a buoyancy force will drive the fluid flow.
Some caution needs to be exercised when making use of the Boussinesq approximation: The only material parameter that is varying is the density 
in the buoyancy term. That means all other occurrences of the density and also the dynamic viscosity 
, the thermal expansion coefficient 
, the specific heat capacity 
and the thermal conductivity 
are constant in the interval 
. The Boussinesq approximation assumes that the pressure is constant. The density in the buoyancy term is a Taylor expansion where 
is the expansion point.
The restrictions pointed out above are quite sever and it is advisable to make sure that the conditions are satisfied. Some effort was made to derive the following criteria [2; 5]:
Here, 
is the maximal temperature fluctuation around 
and 
is a characteristic length.
The following example illustrates this procedure for water [2, p. 133]. To make an estimate of when the approximation is valid, we encode the inequalities from above.
For water at 
and 
we have the following parameters [5]:
The same can be done also considering the pressure [5]. One final remark is that for integrating quantities that involve the material constants, the reference values like 
should be used and not the temperature dependent density 
used in the buoyancy force term [4].
Rayleigh–Bénard convection
As an application to the Boussinesq approximation we present a Rayleigh–Bénard convection. In this example we have a rectangular region filled with a fluid. The side walls are insulated and the top an bottom walls are cooled and heated, respectively. First a region and some parameters are specified.
The rectangle has an aspect ratio of 4:1.
Set up a viscous Navier–Stokes equation that is coupled to a heat equation making use of a Boussinesq approximation. Use the material parameters specified.
Boundary conditions and initial conditions need to be set up.
Monitor the time integration progress and the total time it takes to solve the PDE while using a refined mesh and interpolating the velocities 
and 
and the temperature 
with second order and the pressure 
with first order.
The last step is post-processing.
Further examples for heat transfer with fluid flow can be found in the model collection example Buoyancy Driven Flow where a Reynolds number based model is used and a second example, Heat Exchange that uses a standard model. The example Thermal decomposition shows a coupling of heat, mass and fluid transport.
Flow Boundary Conditions
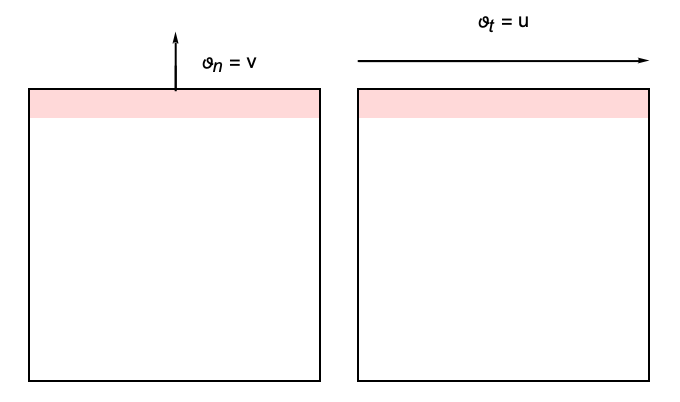
The geometrical domain of a fluid flow model is finite. At the boundaries of the domain we need boundary conditions that model the surroundings in which the flow is embedded. Boundary conditions describe domain walls or inflows into or outflows out of a domain. To make it easier to talk about boundary conditions it is useful to introduce some terminology. Let 
denote a velocity component normal to a boundary and 
denotes a velocity component tangential to a boundary. 
and 
denote the derivatives of both components in the normal direction.
We start be considering a 2D geometry that is parallel to the 
- and 
-axis, like the lid driven cavity example from the introduction. Here we have two cases: Upright boundaries and the horizontal boundaries. For the upright boundary we have:
At a upright boundary, marked in light red, we have a normal fluid flow component 
and tangential fluid flow component 
.
For horizontal boundaries we have:
At a horizontal boundary, marked in light red, we have a normal fluid flow component 
and tangential fluid flow component 
.
In cases where the boundary is not axis-aligned the components 
and 
need to be computed from 
and 
.
Inflow Conditions
An inflow is also called an inlet. Both velocity components are prescribed:
Here 
and 
are the normal and tangential components of the velocity vector 
. To specify the inflow condition 
and 
are given. A typical inflow profile is:
where 
is a function that specifies a fluid velocity in the normal direction.
Outflow Conditions
An outflow is also called an outlet. Both velocity components remains constant with respect to the normal:
Wall Conditions
A wall is any impermeable boundary containing a fluid. One condition at the wall boundary is then that the fluid can not flow through the wall. A minimal requirement then is that:
If only this minimal requirement is satisfied we speak of a slip condition. A second requirement is often that additionally there should be no fluid flow tangential to the wall boundary. In this second case we speak of a no-slip condition.
A typical wall boundary condition is the no-slip condition. No-slip means that first there is no fluid going through the wall and, second, that the fluid adheres to the wall. The second condition models friction at the boundary. In sum this means that:
Thus, the fluid flow velocity vector is set to 0 at this boundary.
This can be set with a DirichletCondition.
This example shows the application of a no-slip wall boundary condition. We have a rectangular flow region with two semi-disk cutouts. On left we have an inflow profile and on the right we have an outflow condition. The remainder of the domain are walls modeled as a no-slip boundary condition.
Note, that at 
and at 
the velocity is 0.
Note, that at 
and at 
the velocity is 0.
In the slip, there is still no fluid going through the wall but contrary to the no-slip condition in the slip case there no loses due to friction this means that:
In the axis-aligned case we have for a upright wall
In the axis-aligned case we have for a horizontal wall
Traction
Let's consider the Navier-Stokes momentum equation:
The viscous stress tensor 
is given as:
When we expand all terms we get:
where 
is the total stress. The total stress is the viscous stress 
plus the pressure component.
We now would like to consider traction boundary conditions. To prescribe traction we would like to specify
where 
is a traction value vector. With all terms substituted:
The total stress tensor 
in component form is:
The type of boundary conditions can be specified through NeumannValue.
The following example considers a flow with a prescribed traction boundary conditions in an annulus region. On the outer at edge, at 
, we have no-slip boundary conditions. These set the fluid velocity in the 
and 
direction to 0, 
.
On the inner boundary, at 
, in stead of defining a velocity, a traction is prescribed. The traction with the stress vector 
is given as:
Here, 
is the radial unit vector given as 
and 
is the tangent unit vector given as 
. 
and 
are the Cartesian unit vectors in the 
-axis and 
-axis direction, respectively. For this example we set the traction in normal direction to 
and the tangential traction 
. This means that we have no flow across the inner boundary but only tangentially to it.
On the outer boundary we have a no-slip condition.
On the inner surface we can compute the tangent unit normal from the outward pointing unit normal 
with a cross product.
To extract the first and second component of the cross product for the 
and 
direction, respectively, we used Indexed.
Equivalently, we note that the tangent unit normal can also be given as 
because the unit normal vector on the inner surface is 
and the unit tangent then is 
.
With out specifying a boundary condition for the pressure, the pressure value will be floating and NDSolve will give a warning that not enough boundary conditions are specified.
To verify that the traction boundary condition works, we can compute radial and tangential components of the velocities and plot them at 
for all 
. For the radial velocity we expect a solution proportional to 
and for the tangential velocity we expect a solution proportional to 
.
Next, we'd like to compute the normal stress and the shear at the inner boundary and check that they match the prescribed traction boundary conditions. The total stress tensor is given by:
The normal and tangential components of traction vector can be computed by
Initial conditions
For time dependent problems initial conditions 
need to be specified.
Initial conditions 
need to satisfy the continuity equation.
Convergence of Fluid Flow Models
Fluid flow PDEs can be difficult to get to converge. This section provides hints at what to try when NDSolve can not find a solution to a fluid flow model. Combinations of the methods presented here are possible.
Initial seeding
Typically nonlinear solvers need an initial guess, a seed to get started. If this seed is too far off from the solution the solver can not converge. The radius in which the solver converges is called the radius of convergence. The closer the initial seed is to the final solution the better.
Here we use the solution of a low Reynolds number flow field to seed the computation of a higher Reynolds number. For this we make use the parametric function.
Specifying the dependent variables, helps the solver to create an optimized system of equations.
Equation modification
This may sound absurd at first, why would you modify equation? Sometimes it is possible that a more stable or reduced set of equations can be used. The solution can then be used as a seed for the full equations.
When no initial seed are specified the solver assumes 0 for all dependent variables. In the case of fluid dynamics, when an initial seed of 0 is used for the velocity field and pressure are used, you are in effect solving a Stokes type equation.
References
1. Simple Fields of Physics; Backstrom, G.; 2006; GB Publishing; ISBN 91-975553-0-4
2. Numerische Simulation in der Strömungsmechanik; Griebel M. et al.; 1995; Vieweg; ISBN 3-528-06761-6
3. The Efficient Engineer; https://www.youtube.com/watch?v=VvDJyhYSJv8; retrieved 2022/12/05
4. On the use and misuse of the Oberbeck–Boussinesq approximation; Barletta, A.; Celli, M; Rees, D.A.S; https://arxiv.org/abs/2202.10981v2; retrieved 2023/03/21
5. The validity of the Boussinesq approximation for liquids and gases; Gray, D.; Giorini, A.; International Journal of Heat and Mass Transfer Volume 19, Issue 5, May 1976, Pages 545-551; https://doi.org/10.1016/0017-9310(76)90168-X
6. “High-Re Solutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method; Ghia, U., Ghia, K.N., Shin, C.T.; Journal of Computational Physics vol. 48, pp. 387–411, 1982.; https://doi.org/10.1016/0021-9991(82)90058-4