FourierDSTMatrix

FourierDSTMatrix[n]

返回类型为 2 的 n×n 离散正弦变换矩阵.

FourierDSTMatrix[n,m]

返回类型为 m 的 n×n 离散正弦变换矩阵.

更多信息和选项

  • 类型为 m 的离散正弦变换矩阵的每个元素 Frs 按下列计算：
  • 1.DST-I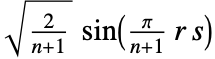
    2.DST-II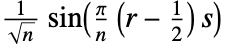
    3.DST-III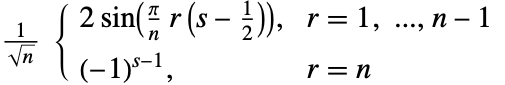
    4.DST-IV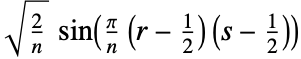
  • 类型为 1、2、3 和 4 的离散正弦变换矩阵分别具有类型为 1、3、2 和 4 的逆. »
  • FourierDSTMatrix 的行是离散正弦变换的基本序列.
  • FourierDSTMatrix[n].list 的结果等价于 FourierDST[list] 当 list 具有长度为 n. 但是，FourierDST[list] 的计算更快，并且具有较少的数值误差. »
  • 对于类型 1 和 4，支持 TargetStructure 选项，该选项指定返回矩阵的结构. TargetStructure 的可能设置包括：
  • Automatic自动选择返回的表示
    "Dense"以稠密矩阵的形式表示矩阵
    "Hermitian"以埃尔米特矩阵 (Hermitian matrix) 的形式表示矩阵
    "Orthogonal"以正交矩阵的形式表示矩阵
    "Symmetric"以对称矩阵的形式表示矩阵
    "Unitary"以酉矩阵的形式表示矩阵
  • FourierDSTMatrix[…,TargetStructureAutomatic] 等价于 FourierDSTMatrix[…,TargetStructure"Dense"].
  • FourierDSTMatrix[…,WorkingPrecision->p] 给出元素精度为 p 的矩阵.

范例

打开所有单元关闭所有单元

基本范例  (1)

一个 4×4 离散正弦变换矩阵：

范围  (1)

长度为 128 的离散正弦变换的基本序列：

选项  (2)

TargetStructure  (1)

以稠密矩阵的形式返回 DST 矩阵：

以正交矩阵的形式返回 DST 矩阵：

以对称矩阵的形式返回 DST 矩阵：

WorkingPrecision  (1)

使用机器精度：

使用任意精度：

应用  (1)

一个三对角托普利兹（Toeplitz matrix）矩阵：

其特征向量矩阵可以表示为对角重新缩放的 1 型离散正弦变换矩阵：

对角化三对角矩阵：

属性和关系  (2)

离散正弦变换矩阵乘以向量等价于计算该向量的离散正弦变换：

FourierDST 比基于矩阵的计算更快：

类型为 1 的离散正弦变换矩阵是它自身的逆：

类型为 3 的离散正弦变换矩阵是类型为2的矩阵的逆：

类型为 4 的离散正弦变换矩阵是它自身的逆：

Wolfram Research (2012)，FourierDSTMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierDSTMatrix.html （更新于 2024 年）.

文本

Wolfram Research (2012)，FourierDSTMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierDSTMatrix.html （更新于 2024 年）.

CMS

Wolfram 语言. 2012. "FourierDSTMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FourierDSTMatrix.html.

APA

Wolfram 语言. (2012). FourierDSTMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FourierDSTMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_fourierdstmatrix, author="Wolfram Research", title="{FourierDSTMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDSTMatrix.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourierdstmatrix, organization={Wolfram Research}, title={FourierDSTMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/FourierDSTMatrix.html}, note=[Accessed: 23-November-2024 ]}