FourierMatrix

FourierMatrix[n]

returns an n×n Fourier matrix.

Details and Options

  • FourierMatrix of order n returns a list of the length-n discrete Fourier transform's basis sequences.
  • Each entry of the Fourier matrix is by default defined as 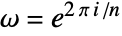, where .
  • Rows of the FourierMatrix are basis sequences of the discrete Fourier transform.
  • The result F of FourierMatrix[n] is complex symmetric and unitary, meaning that F-1 is Conjugate[F].
  • The following options can be given:
  • FourierParameters {0,1}parameters to define the Fourier transform
    TargetStructure Automaticthe structure of the returned matrix
    WorkingPrecision Infinityprecision at which to create entries
  • Different choices of definitions for the Fourier matrix can be specified using the option FourierParameters. With the setting FourierParameters->{a,b}, the Fourier matrix has entries defined as 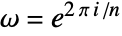, where .
  • Some common choices for {a,b} are {0,1} (physics), {-1,1} (data analysis), {1,-1} (signal processing).
  • Possible settings for TargetStructure include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Structured"represent the matrix as a structured array
  • With FourierMatrix[…,TargetStructureAutomatic], a dense matrix is returned if the number of matrix entries is less than a preset threshold, and a structured array is returned otherwise.
  • The result of FourierMatrix[n].list is equivalent to Fourier[list] when list has length n. However, the computation of Fourier[list] is much faster and has less numerical error, unless FourierMatrix is kept as a structured array. »
  • For a structured FourierMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
  • "FourierParameters"parameters {a,b}
    "WorkingPrecision"precision used internally
    "Properties"list of supported properties
    "Structure"type of structured array
    "StructuredData"internal data stored by the structured array
    "StructuredAlgorithms"list of functions with special methods for the structured array
    "Summary"summary information, represented as a Dataset

Examples

open allclose all

Basic Examples  (2)

A Fourier matrix:

A large Fourier matrix:

Scope  (2)

The real and imaginary parts of the Fourier's basis sequences of length 128:

Construct a structured Fourier matrix using the option setting TargetStructure"Structured":

The structured representation saves a significant amount of memory for larger matrices:

Options  (3)

FourierParameters  (1)

The default definition of the Fourier matrix:

Use the definition of the Fourier matrix used in signal processing:

Use the definition of the Fourier matrix used in data analysis:

TargetStructure  (1)

Return the Fourier matrix as a dense matrix:

Return the Fourier matrix as a structured array:

WorkingPrecision  (1)

Use machine precision:

Use arbitrary precision:

Applications  (3)

The efficiency of the fast Fourier transform (FFT) relies on being able to form a larger Fourier matrix from two smaller ones. Generate two small Fourier matrices of sizes p and q:

The Fourier matrix of size p q can be expressed as a product of four simpler matrices:

Show that the resulting matrix is equivalent to the result of FourierMatrix:

The discrete Fourier transform of a vector can be computed by successively multiplying the factors of the Fourier matrix to the vector:

The result is equivalent to applying Fourier to the vector:

Define a function for constructing a circulant matrix from a vector:

Circulant matrices can be diagonalized by the Fourier matrix:

The diagonal elements of the resulting diagonal matrix are the same as the product of the Fourier matrix and the starting vector, up to a constant scaling factor:

A Fourier matrix with unit normalization:

For even dimensions, the permanent of the matrix is zero:

For odd dimensions, the permanent of the matrix is always an integer:

For an odd prime p>3, the permanent of the p×p matrix is congruent to p!, modulo p3:

Properties & Relations  (2)

FourierMatrix can be represented as a scaled VandermondeMatrix:

The Fourier transform of a vector is equivalent to the vector multiplied by a Fourier matrix:

The inverse Fourier transform is equivalent to multiplying by the conjugate transpose:

Fourier is much faster than the matrix-based computation:

Wolfram Research (2012), FourierMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierMatrix.html.

Text

Wolfram Research (2012), FourierMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierMatrix.html.

CMS

Wolfram Language. 2012. "FourierMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierMatrix.html.

APA

Wolfram Language. (2012). FourierMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierMatrix.html

BibTeX

@misc{reference.wolfram_2023_fouriermatrix, author="Wolfram Research", title="{FourierMatrix}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FourierMatrix.html}", note=[Accessed: 10-December-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_fouriermatrix, organization={Wolfram Research}, title={FourierMatrix}, year={2012}, url={https://reference.wolfram.com/language/ref/FourierMatrix.html}, note=[Accessed: 10-December-2023 ]}