InverseFourier

InverseFourier[list]

finds the discrete inverse Fourier transform of a list of complex numbers.

InverseFourier[list,{p1,p2,…}]

returns the specified positions of the discrete inverse Fourier transform.

Details and Options

  • The inverse Fourier transform 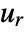of a list 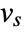of length 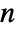is defined to be . »
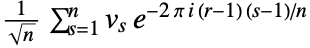  • Note that the zero frequency term must appear at position 1 in the input list.
  • Other definitions are used in some scientific and technical fields.
  • Different choices of definitions can be specified using the option FourierParameters.
  • With the setting FourierParameters->{a,b} the discrete Fourier transform computed by InverseFourier is .
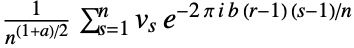  • Some common choices for {a,b} are {0,1} (default), {-1,1} (data analysis), {1,-1} (signal processing).
  • The setting b=-1 effectively corresponds to conjugating both input and output lists.
  • To ensure a unique discrete Fourier transform, Abs[b] must be relatively prime to .
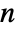  • The list of data need not have a length equal to a power of two.
  • The list given in InverseFourier[list] can be nested to represent an array of data in any number of dimensions.
  • The array of data must be rectangular.
  • InverseFourier[list,{p1,p2,…}] is typically equivalent to Extract[InverseFourier[list],{p1,p2,…}]. Cases with just a few positions p are computed using an algorithm that takes less time and memory but is more subject to numerical error, particularly when the length of list is long.
  • If the elements of list are exact numbers, InverseFourier begins by applying N to them.

Examples

open allclose all

Basic Examples  (2)

Inverse Fourier transform of a real list:

Inverse Fourier transform of a complex list:

Scope  (3)

x is a list of real values:

Compute the inverse Fourier transform with machine arithmetic:

Compute using 24-digit precision arithmetic:

Compute a 2D inverse Fourier transform:

x is a rank-4 tensor with a single nonzero entry:

Compute the 4D inverse Fourier transform:

Options  (3)

FourierParameters  (3)

No normalization:

Normalization by :

Normalization by :

InverseFourier is the same as Fourier with parameter :

Data from a sinc function with noise:

Get the Fourier transform:

Reconstruct the signal from part of the spectrum:

Applications  (1)

Some Gaussian data:

The multiplication of each mode to get the first derivative:

Approximate the first derivative of the data:

Note the derivative approximation implicitly assumes periodicity:

Properties & Relations  (2)

is given by :

InverseFourier is equivalent to multiplication with FourierMatrix with specified parameters:

The conjugate transpose of the matrix is equivalent to Fourier:

Possible Issues  (1)

InverseFourier uses an efficient algorithm when only a small number of coefficients is needed:

The fast and efficient implementation may result in significant numerical error:

Wolfram Research (1988), InverseFourier, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseFourier.html (updated 2012).

Text

Wolfram Research (1988), InverseFourier, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseFourier.html (updated 2012).

CMS

Wolfram Language. 1988. "InverseFourier." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2012. https://reference.wolfram.com/language/ref/InverseFourier.html.

APA

Wolfram Language. (1988). InverseFourier. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseFourier.html

BibTeX

@misc{reference.wolfram_2024_inversefourier, author="Wolfram Research", title="{InverseFourier}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/InverseFourier.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inversefourier, organization={Wolfram Research}, title={InverseFourier}, year={2012}, url={https://reference.wolfram.com/language/ref/InverseFourier.html}, note=[Accessed: 17-November-2024 ]}