FourierSinSeries
FourierSinSeries[expr,t,n]
给出关于 t 的 expr 的 n 阶傅立叶正弦级数展开式.
FourierSinSeries[expr,{t1,t2,…},{n1,n2,…}]
给出一个expr 多维傅立叶正弦级数.
更多信息和选项

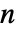 阶傅立叶正弦级数展开式
阶傅立叶正弦级数展开式 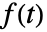 默认是
默认是 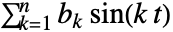 ,其中
,其中 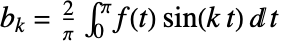 .
.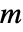 维傅立叶正弦系数
维傅立叶正弦系数 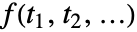 由
由 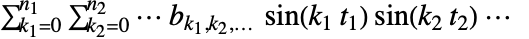 给出,其中
给出,其中 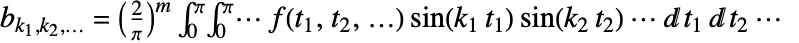 .
.- 可以给出下列选项:
-
Assumptions $Assumptions 参数的假设 FourierParameters {1,1} 定义傅立叶级数的参数 GenerateConditions False 是否产生关于参数条件的结果 - FourierParameters 的普通设置是:
-
{1,1} 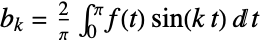
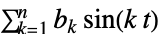
{1,2Pi} 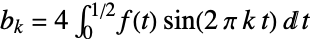
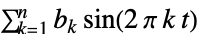
{a,b} 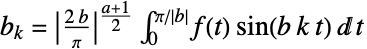
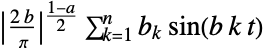
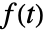 傅立叶正弦级数等价于
傅立叶正弦级数等价于 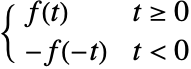 的傅立叶级数.
的傅立叶级数.
范例
打开所有单元关闭所有单元选项 (1)
FourierParameters (1)
对 FourierParameters 使用一个非缺省设置:
Wolfram Research (2008),FourierSinSeries,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FourierSinSeries.html.
文本
Wolfram Research (2008),FourierSinSeries,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FourierSinSeries.html.
CMS
Wolfram 语言. 2008. "FourierSinSeries." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FourierSinSeries.html.
APA
Wolfram 语言. (2008). FourierSinSeries. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FourierSinSeries.html 年