FunctionBijective[f,x]
tests whether ![]() has exactly one solution x∈Reals for each y∈Reals.
has exactly one solution x∈Reals for each y∈Reals.
FunctionBijective[f,x,dom]
tests whether ![]() has exactly one solution x∈dom for each y∈dom.
has exactly one solution x∈dom for each y∈dom.
FunctionBijective[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() has exactly one solution x1,x2,…∈dom for each y1,y2,…∈dom.
has exactly one solution x1,x2,…∈dom for each y1,y2,…∈dom.
FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom]
tests whether ![]() has exactly one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
has exactly one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.


FunctionBijective
FunctionBijective[f,x]
tests whether ![]() has exactly one solution x∈Reals for each y∈Reals.
has exactly one solution x∈Reals for each y∈Reals.
FunctionBijective[f,x,dom]
tests whether ![]() has exactly one solution x∈dom for each y∈dom.
has exactly one solution x∈dom for each y∈dom.
FunctionBijective[{f1,f2,…},{x1,x2,…},dom]
tests whether ![]() has exactly one solution x1,x2,…∈dom for each y1,y2,…∈dom.
has exactly one solution x1,x2,…∈dom for each y1,y2,…∈dom.
FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom]
tests whether ![]() has exactly one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
has exactly one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.
Details and Options

- A bijective function is also known as one-to-one and onto.
- A function
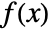 is bijective if for each
is bijective if for each 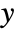 there is exactly one
there is exactly one 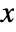 such that
such that 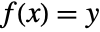 .
. - FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom] returns True if the mapping
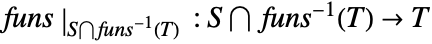 is bijective, where
is bijective, where 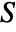 is the solution set of xcons and
is the solution set of xcons and 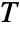 is the solution set of ycons.
is the solution set of ycons. - If funs contains parameters other than xvars, the result is typically a ConditionalExpression.
- Possible values for dom are Reals and Complexes. If dom is Reals, then all variables, parameters, constants and function values are restricted to be real.
- The domain of funs is restricted by the condition given by FunctionDomain.
- xcons and ycons can contain equations, inequalities or logical combinations of these.
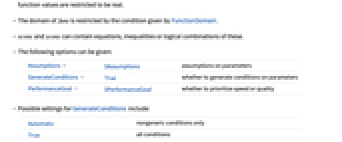
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions True whether to generate conditions on parameters PerformanceGoal $PerformanceGoal whether to prioritize speed or quality - Possible settings for GenerateConditions include:
-
Automatic nongeneric conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal are "Speed" and "Quality".

Examples
open all close allBasic Examples (4)
Scope (10)
Some values are attained more than once:
Bijectivity between subsets of the reals:
For ![]() , each positive value is attained exactly once:
, each positive value is attained exactly once:
Bijectivity over the complexes:
The logarithm is bijective onto ![]() :
:
Bijectivity over a subset of complexes:
![]() is not bijective over the whole complex plane:
is not bijective over the whole complex plane:
Some values are attained more than once:
Bijectivity over the integers:
Bijectivity of linear mappings:
A linear mapping is bijective iff its matrix is square and of the maximal rank:
Bijectivity of polynomial mappings ![]() :
:
The restricted mapping ![]() , equal to the real and imaginary part of
, equal to the real and imaginary part of ![]() , is bijective:
, is bijective:
Bijectivity of polynomial mappings ![]() :
:
The Jacobian determinant of a bijective complex polynomial mapping must be constant:
The Jacobian conjecture states that the reverse implication is true:
Indeed, this polynomial mapping with a constant Jacobian is bijective:
Bijectivity of a real polynomial with symbolic parameters:
Bijectivity of a real polynomial mapping with symbolic parameters:
Options (4)
Assumptions (1)
FunctionBijective gives a conditional answer here:
This checks the bijectivity for the remaining real values of ![]() :
:
GenerateConditions (2)
By default, FunctionBijective may generate conditions on symbolic parameters:
With GenerateConditions->None, FunctionBijective fails instead of giving a conditional result:
This returns a conditionally valid result without stating the condition:
By default, all conditions are reported:
With GenerateConditions->Automatic, conditions that are generically true are not reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
Applications (11)
Basic Applications (8)
Each value is attained exactly once:
Some values, e.g. ![]() , are attained more than once:
, are attained more than once:
Some values, e.g. ![]() , are not attained:
, are not attained:
![]() is bijective in its real domain:
is bijective in its real domain:
Each value is attained exactly once:
A function is bijective iff it is injective and surjective:
![]() is not bijective because it is not injective:
is not bijective because it is not injective:
![]() is not bijective because it is not surjective:
is not bijective because it is not surjective:
A function is bijective if any horizontal line intersects the graph exactly once:
Some horizontal lines intersect the graph more than once; others do not intersect it at all:
Composition of bijective functions ![]() is bijective:
is bijective:
An affine mapping ![]() given by
given by ![]() is bijective if the rank of
is bijective if the rank of ![]() equals
equals ![]() :
:
Probability (1)
CDF of a distribution with a strictly positive PDF is bijective onto ![]() :
:
SurvivalFunction is bijective onto ![]() as well:
as well:
Quantile is bijective onto the reals:
Calculus (2)
Compute ![]() by change of variables:
by change of variables:
If ![]() is a bijective mapping
is a bijective mapping ![]() , then
, then ![]() :
:
Check that ![]() is a bijective mapping
is a bijective mapping ![]() :
:
Compute the original integral directly:
Compute the surface area of a ball with radius ![]() using a rational parametrization:
using a rational parametrization:
Check that the parametrization is bijective onto the ball less a lower-dimensional set:
The surface area is equal to the integral of square root of Gram determinant of ![]() :
:
Properties & Relations (3)
![]() is bijective iff the equation
is bijective iff the equation ![]() has exactly one solution for each
has exactly one solution for each ![]() :
:
Use Solve to find the solutions:
A real continuous function on an interval is bijective iff it is monotonic and the limits at endpoints are ![]() and
and ![]() :
:
Use FunctionMonotonicity to determine the monotonicity of a function:
Use Limit to compute the limits:
A complex polynomial mapping is bijective iff it has a polynomial inverse:
Use Solve to find the polynomial inverse:
Possible Issues (2)
FunctionBijective determines the real domain of functions using FunctionDomain:
![]() is bijective onto
is bijective onto ![]() in the real domain reported by FunctionDomain:
in the real domain reported by FunctionDomain:
![]() is real valued and not bijective onto
is real valued and not bijective onto ![]() over the whole reals:
over the whole reals:
All subexpressions of ![]() need to be real valued for a point to belong to the real domain of
need to be real valued for a point to belong to the real domain of ![]() :
:
FunctionBijective restricts the domain to the inverse image of the solution set of ycons:
Division by two is a bijection between the even integers (the inverse image of integers) and the integers.
Related Guides
History
Text
Wolfram Research (2020), FunctionBijective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionBijective.html.
CMS
Wolfram Language. 2020. "FunctionBijective." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionBijective.html.
APA
Wolfram Language. (2020). FunctionBijective. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionBijective.html
BibTeX
@misc{reference.wolfram_2025_functionbijective, author="Wolfram Research", title="{FunctionBijective}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionBijective.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_functionbijective, organization={Wolfram Research}, title={FunctionBijective}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionBijective.html}, note=[Accessed: 08-January-2026]}