FunctionMonotonicity

FunctionMonotonicity[f,x]

finds the monotonicity of the function f with the variable x over the reals.

FunctionMonotonicity[f,x,dom]

finds the monotonicity of f when x is restricted to the domain dom.

FunctionMonotonicity[{f,cons},x,dom]

gives the monotonicity of f when x is restricted by the constraints cons.

Details and Options

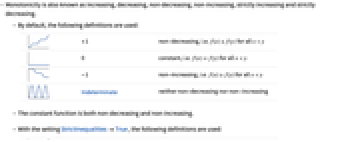
  • Monotonicity is also known as increasing, decreasing, non-decreasing, non-increasing, strictly increasing and strictly decreasing.
  • By default, the following definitions are used:
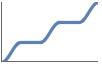
  • +1non-decreasing, i.e. 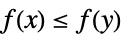for all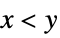
    0constant, i.e. 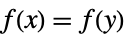for all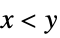
    -1non-increasing, i.e. 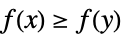for all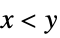
    Indeterminateneither non-decreasing nor non-increasing
  • The constant function is both non-decreasing and non-increasing.
  • With the setting StrictInequalitiesTrue, the following definitions are used:
  • +1increasing, i.e. 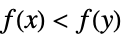for all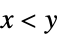
    -1decreasing, i.e. 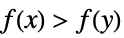for all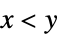
    Indeterminateneither increasing nor decreasing
  • Possible values for dom include: Reals, Integers, PositiveReals, PositiveIntegers, etc. The default is Reals.
  • The function f should be a real-valued function for all x in the domain dom that satisfy the constraints cons.
  • cons can contain equations, inequalities or logical combinations of these.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Truewhether to generate conditions on parameters
    PerformanceGoal $PerformanceGoalwhether to prioritize speed or quality
    StrictInequalities Truewhether to require strict monotonicity
  • Possible settings for GenerateConditions include:
  • Automaticnongeneric conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal are "Speed" and "Quality".

Examples

open allclose all

Basic Examples  (3)

Find the monotonicity of a function:

Find the monotonicity of a function with the variable restricted by constraints:

Find the monotonicity of a function over the integers:

Scope  (5)

Monotonicity over unrestricted reals:

A function that is not real valued has Indeterminate monotonicity:

The function is real valued and increasing for positive :

Monotonicity with constraints on the variable:

Strict monotonicity of a function:

TemplateBox[{x}, Floor] is non-decreasing, but not strictly increasing. TemplateBox[{x}, Floor]+x is strictly increasing:

Functions with symbolic parameters:

Options  (5)

Assumptions  (1)

FunctionMonotonicity gives a conditional answer here:

Check monotonicity for other values of :

GenerateConditions  (2)

By default, FunctionMonotonicity may generate conditions on symbolic parameters:

With GenerateConditionsNone, FunctionMonotonicity fails instead of giving a conditional result:

This returns a conditionally valid result without stating the condition:

By default, all conditions are reported:

With GenerateConditionsAutomatic, conditions that are generically true are not reported:

PerformanceGoal  (1)

Use PerformanceGoal to avoid potentially expensive computations:

The default setting uses all available techniques to try to produce a result:

StrictInequalities  (1)

By default, FunctionMonotonicity computes the non-strict monotonicity:

With StrictInequalitiesTrue, FunctionMonotonicity computes the strict monotonicity:

Ramp[x]+1 is non-decreasing, but is not strictly increasing. Ramp[x]+x is strictly increasing:

Applications  (19)

Basic Cases  (5)

Positive powers are all non-decreasing for the positive reals TemplateBox[{}, PositiveReals]:

This shows that the whole family is non-decreasing:

In fact, they are all increasing:

Negative powers are non-increasing for the positive reals TemplateBox[{}, PositiveReals]:

This shows that the whole family is decreasing:

Exponential functions are increasing for and decreasing for :

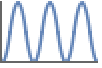
Trigonometric functions are non-monotonic over the reals:

But over smaller ranges they are monotone:

TemplateBox[{x}, Ceiling] is non-decreasing but not increasing:

Combination Cases  (5)

The sum of functions with monotonicity has monotonicity :

The sum has the same monotonicity:

The product of non-negative non-decreasing functions is non-decreasing:

Their product is also non-decreasing:

The composition of non-decreasing functions is non-decreasing:

Their compositions are also non-decreasing:

The inverse of an increasing function is increasing:

The inverse is also increasing:

The range of a non-decreasing function on an interval is :

For comparison, compute the range using FunctionRange:

Calculus  (4)

Prove that has a limit for :

is non-decreasing and bounded from above for :

The limit of at equals the supremum of :

Prove convergence of :

Terms of the series are non-negative, hence the partial sums are increasing:

The partial sums are bounded from above, hence the series converges:

Use Sum to compute the sum of the series:

If is non-negative, then is a non-decreasing function of :

Write a differentiable function as a sum of an increasing function and a decreasing function:

Check whether the functions need to be adjusted by a constant:

Test monotonicity of and :

Probability  (3)

CDF is always non-decreasing:

SurvivalFunction is always non-increasing:

Quantile is always non-decreasing in :

Equation Solving and Optimization  (2)

If is increasing and continuous in and , then has exactly one root in :

Use Solve to find the root:

Compute the maximum of when is a non-decreasing function:

Compute the maximum of :

The maximum value of is and is attained at :

For comparison, compute the maximum directly:

Properties & Relations  (2)

The sum and composition of non-decreasing functions are non-decreasing:

The derivative of a non-decreasing function is non-negative:

Use D to compute the derivative:

Use FunctionSign to verify that the derivative is non-negative:

Plot the function and the derivative:

Possible Issues  (1)

A function must be defined everywhere to be monotonic:

Wolfram Research (2020), FunctionMonotonicity, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionMonotonicity.html.

Text

Wolfram Research (2020), FunctionMonotonicity, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionMonotonicity.html.

CMS

Wolfram Language. 2020. "FunctionMonotonicity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionMonotonicity.html.

APA

Wolfram Language. (2020). FunctionMonotonicity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionMonotonicity.html

BibTeX

@misc{reference.wolfram_2024_functionmonotonicity, author="Wolfram Research", title="{FunctionMonotonicity}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionMonotonicity.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionmonotonicity, organization={Wolfram Research}, title={FunctionMonotonicity}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionMonotonicity.html}, note=[Accessed: 21-November-2024 ]}