FunctionContinuous

FunctionContinuous[f,x]

tests whether is a real-valued continuous function for x∈Reals.

FunctionContinuous[f,x,dom]

tests whether is a continuous function for x∈dom.

FunctionContinuous[{f1,f2,…},{x1,x2,…},dom]

tests whether are continuous functions for x1,x2,…∈dom.

FunctionContinuous[{funs,cons},xvars,dom]

tests whether are continuous functions for xvars∈dom restricted by the constraints cons.

Details and Options

  • A function 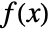is continuous in a set 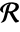if for all 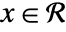and for all 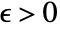there is a 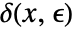such that for all 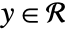, TemplateBox[{{x, -, y}}, Abs]<delta(x,epsilon) implies TemplateBox[{{{f, (, x, )}, -, {f, (, y, )}}}, Abs]<epsilon.
  • A function 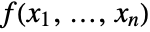is continuous in a set 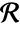if for all 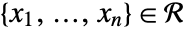and for all 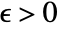there is a 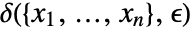such that for all 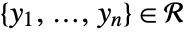, TemplateBox[{{{, {{{x, _, 1}, -, {y, _, 1}}, ,, ..., ,, {{x, _, n}, -, {y, _, n}}}, }}}, Norm]<delta({x_1,...,x_n},epsilon) implies TemplateBox[{{{f, (, {{, {{x, _, 1}, ,, ..., ,, {x, _, n}}, }}, )}, -, {f, (, {{, {{y, _, 1}, ,, ..., ,, {y, _, n}}, }}, )}}}, Abs]<epsilon.
  • If funs contains parameters other than xvars, the result is typically a ConditionalExpression.
  • Possible values for dom are Reals and Complexes. The default is Reals.
  • If dom is Reals, then all variables, parameters, constants and function values are restricted to be real.
  • cons can contain equations, inequalities or logical combinations of these.
  • The functions funs need to be defined for all values that satisfy the constraints cons.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Truewhether to generate conditions on parameters
    PerformanceGoal $PerformanceGoalwhether prioritize speed or quality
  • Possible settings for GenerateConditions include:
  • Automaticnongeneric conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal are "Speed" and "Quality".

Examples

open allclose all

Basic Examples  (4)

Test continuity of real functions:

Test continuity of complex functions:

Test continuity over restricted domains:

Test continuity of multivariate functions:

Scope  (6)

Real univariate functions:

Complex univariate functions:

Functions with restricted domains:

Real multivariate functions:

Complex multivariate functions:

Functions with symbolic parameters:

Options  (4)

Assumptions  (1)

FunctionContinuous cannot find the answer for arbitrary values of the parameter :

With the assumption that , FunctionContinuous succeeds:

GenerateConditions  (2)

By default, FunctionContinuous may generate conditions on symbolic parameters:

With GenerateConditionsNone, FunctionContinuous fails instead of giving a conditional result:

This returns a conditionally valid result without stating the condition:

By default, all conditions are reported:

With GenerateConditionsAutomatic, conditions that are generically true are not reported:

PerformanceGoal  (1)

Use PerformanceGoal to avoid potentially expensive computations:

The default setting uses all available techniques to try to produce a result:

Applications  (14)

Classes of Continuous Functions  (6)

Polynomials are continuous:

Sin, Cos and Exp are continuous:

Visualize these functions:

These functions are continuous in the complex plane as well:

Visualize these functions over TemplateBox[{}, Complexes]:

The reciprocal of a continuous function is continuous wherever :

Thus, rational functions may or may not be continuous over the reals:

However, as every nonconstant polynomial has a root in the plane, rational functions are never continuous on TemplateBox[{}, Complexes]:

Visualizing the function in the complex plane shows the blowup at :

As Cot and Csc are rational functions of Sin and Cos, they are continuous when sine is nonzero:

Visualize the functions along with sine:

Similarly, Tan and Sec are continuous when cosine is nonzero:

This same principle applies to the hyperbolic trigonometric functions Coth and Csch:

Visualize the functions along with Sinh:

As Cosh is never zero, the remaining two functions, Tanh and Sech, are continuous:

The compositions of continuous functions are continuous:

A composition of a discontinuous function and a continuous function will be continuous as long as maps the domain into a continuous subdomain of . Let, for example, be Sqrt. Sqrt is discontinuous on the reals:

However, it is continuous on TemplateBox[{}, PositiveReals]:

Exp maps TemplateBox[{}, Reals]->TemplateBox[{}, PositiveReals]:

Thus, the composition of Sqrt with Exp is continuous on TemplateBox[{}, Reals]:

Multivariate polynomials are continuous over the reals and complexes:

Rational multivariate functions may or may not be continuous over the reals:

They are always discontinuous over the complexes:

Sometimes a discontinuous rational function can be extended to a continuous one:

By composing with continuous univariate functions, many more continuous functions can be generated:

Visualize the continuous functions:

Calculus  (5)

For continuous functions, limits can be computed by substitution:

The functions and agree on the real line except at zero:

Sinc is continuous:

The function is not continuous:

In particular, it is discontinuous at the origin, so its limit there cannot be computed by substitution:

Since the two functions are equal for , they have the same limit there:

The following function is discontinuous:

Its only discontinuity is at the origin:

The discontinuity results from being undefined there:

However, has a limit as :

Define as an extension of to the origin:

This extension is a continuous function:

Visualize :

The function is continuous:

However, its first derivative is not continuous:

Therefore, is not analytic:

While goes smoothly to zero, its derivative oscillates wildly at the origin:

Visualize and its first derivative:

The definite integral of a bounded function is continuous, even if is discontinuous. Consider the following :

It is discontinuous:

Define to be its definite integral from the origin to an arbitrary real value:

The function is continuous

Visualize the function and its integral:

Probability  (3)

The CDF of a continuous probability distribution is continuous:

Visualize the functions:

The CDF of a discrete distribution is discontinuous:

These distributions have piecewise-constant cumulative distribution functions:

The CDF of a mixed distribution is discontinuous:

These distributions have piecewise, but nonconstant, cumulative distribution functions:

Properties & Relations  (3)

At each point of the domain, the limit of a continuous function is equal to its value:

Use Limit to compute limits:

A function continuous in an interval attains each value between its minimum and maximum:

Use Minimize and Maximize to find minima and maxima:

Check that is between the minimum and the maximum:

Use Solve to find the points where attains the value :

Illustrate the property:

Use FunctionAnalytic to check whether a function is analytic:

Analytic functions are continuous:

Continuous functions may not be analytic:

Possible Issues  (2)

A function needs to be defined everywhere to be continuous:

A function needs to be real valued to be continuous over the real domain:

Wolfram Research (2020), FunctionContinuous, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionContinuous.html.

Text

Wolfram Research (2020), FunctionContinuous, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionContinuous.html.

CMS

Wolfram Language. 2020. "FunctionContinuous." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionContinuous.html.

APA

Wolfram Language. (2020). FunctionContinuous. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionContinuous.html

BibTeX

@misc{reference.wolfram_2024_functioncontinuous, author="Wolfram Research", title="{FunctionContinuous}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionContinuous.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functioncontinuous, organization={Wolfram Research}, title={FunctionContinuous}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionContinuous.html}, note=[Accessed: 17-November-2024 ]}