FunctionInjective

FunctionInjective[f,x]

が各 y について最大1個の解 x∈Realsを持つかどうかを調べる．

FunctionInjective[f,x,dom]

が最大1個の解 x∈dom を持つかどうかを調べる．

FunctionInjective[{f1,f2,…},{x1,x2,…},dom]

が最大1個の解 x1,x2,…∈dom を持つかどうかを調べる．

FunctionInjective[{funs,xcons,ycons},xvars,yvars,dom]

が，条件 ycons で制約された各 yvars∈dom に対して条件 xcons で制約された最大1個の解 xvars∈dom を持つかどうかを調べる．

詳細とオプション

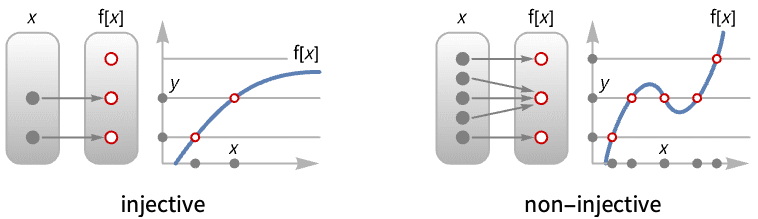
  • 単射関数は一対一の関数としても知られている．
  • 各 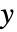に対して 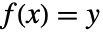となる最大で1つの 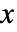がある場合，関数 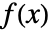は単射である．
  • 写像 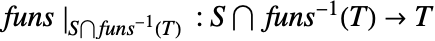が単射ならFunctionInjective[{funs,xcons,ycons},xvars,yvars,dom]はTrueを返す．ただし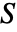， は xcons の解集合で は ycons の解集合である．
  • funs が xvars 以外のパラメータを含むなら，結果は，一般に，ConditionalExpressionである．
  • dom の可能な値にはRealsとComplexesがある．dom がRealsのときは，変数，パラメータ，定数，関数値がすべて実数でなければならない．
  • funs の領域はFunctionDomainが与える条件によって制限される．
  • xcons と ycons は，等式，不等式，あるいはそれらの論理結合を含むことができる．
  • 次は，使用可能なオプションである，
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Trueパラメータについての条件を生成するかどうか
    PerformanceGoal $PerformanceGoal速度と品質のどちらを優先するか
  • 次は，GenerateConditionsの可能な設定である．
  • Automatic一般的ではない条件のみ
    Trueすべての条件
    False条件なし
    None条件が必要な場合は未評価で返す
  • PerformanceGoalの可能な値は"Speed"と"Quality"である．

例題

すべて開くすべて閉じる

例  (4)

1変数関数の実領域における単射性を調べる：

複素領域における単射性を調べる：

多項式の実数への写像の単射性を調べる：

記号係数を持つ多項式の単射性を調べる：

スコープ  (12)

実数への単射性：

複数回出現する値もある：

実数の部分集合に対する単射性：

については，各値は最大1回出現する：

実数の部分集合の逆像に対する単射性：

のとき， の各値は最大1回出現する：

複素数に対する単射性：

各値は最大1回出現する：

複素数の部分集合に対する単射性：

は複素平面全体に対しては単射ではない：

複数回出現する値もある：

整数に対する単射性：

線形写像の単射性：

線形写像は，その行列の階数が領域の次元と等しいときかつそのときに限り単射である：

多項式写像の単射性：

各値は最大1回出現する：

この写像は単射ではない：

複数回出現する値がある：

多項式写像の単射性：

の実部と虚部に等しい写像は，非負の象限において単射である：

多項式写像の単射性：

単射複素多項式写像のヤコビ行列式は定数でなければならない：

ヤコビアン予想には逆の予想が真であるとある：

たしかに，定数のヤコビ行列式がある多項式写像は単射である：

記号パラメータを持つ実多項式の単射性：

記号パラメータを持つ実多項式写像の単射性：

オプション  (4)

Assumptions  (1)

FunctionInjectiveは，任意の について TemplateBox[{n, x}, BesselI]の単射性を決定できない：

が奇整数であると仮定するとFunctionInjectiveはうまくいく：

GenerateConditions  (2)

デフォルトで，FunctionInjectiveは記号パラメータについての条件を生成することがある：

GenerateConditionsNoneとすると，FunctionInjectiveは条件付きの結果を与えることができない：

以下は，条件下で有効な結果を条件を示さずに返す：

デフォルトで，すべての条件が報告される：

GenerateConditionsAutomaticのときは，一般的に真である条件は報告されない：

PerformanceGoal  (1)

PerformanceGoalを使って潜在的に高くつく計算を回避する：

デフォルト設定は使用可能なあらゆるテクニックを使って結果を出そうとする：

アプリケーション  (17)

基本的なアプリケーション  (8)

の単射性をチェックする：

値は複数回出現するので，は単射ではない：

の単射性をチェックする：

どの値も最大1回出現する：

実領域におけるの単射性をチェックする：

は，その実領域において単射である：

制限のない実部におけるClip[x]の単射性をチェックする：

値とは，それぞれ[-∞,-1]と[1, ∞]に複数回出現する：

区間[-1, 1]に制限されたClip[x]は単射である：

任意の水平線がグラフと最大1回しか交差しない関数は単射である：

水平線がグラフと複数回交差する関数は単射ではない：

周期関数は単射ではない：

FunctionPeriodを使って関数が周期的かどうかをチェックする：

周期関数は各値に無限回出現する：

導関数の符号が正または負に固定されている関数は単射である：

FunctionSignを使って導関数の符号を求める：

次の関数は厳密に増加しており，したがって単射である：

符号が正または負に固定されている関数の積分は単射である：

正の区分関数を[0,2]で引数値について積分する：

この積分は0≤x≤2のとき単射である：

単射関数は連続または単調である必要はない：

連続単射関数が単調である必要はない：

この関数は連続関数だが，その領域は連結集合ではない：

写像の単射性をチェックする：

ParametricPlotの一部は2回変換されている：

正の と についての写像は単射である：

ParametricPlotの各点は1回しかカバーされない：

以下では，点{0,0}が明らかに複数回カバーされている：

これらはどれも， と が{0,0}に写像されたものである：

これを除くと写像は単射である：

方程式と不等式を解く  (4)

の任意の値について方程式 が についての解を最大1個持つとき，は単射である：

の解は1つである：

の解はない：

の解は最大1個である：

写像 は単射ではない：

方程式 には2つの解がある：

という制約がある は単射である：

方程式 は，のときは最大1個の解を持つ：

任意の単射関数 には逆関数がある：

逆関数の定義域は の値域である：

連結集合上で定義される非零の微分を持つ微分可能な関数は単射である：

の導関数は のとき正である：

は のとき単射である：

の逆関数は方程式 を満足する：

結果が，のとき実際に の逆関数であることを確かめる：

確率と統計  (2)

厳密に正のPDFを持つ分布のCDFは単射である：

SurvivalFunctionとQuantileも単射である：

微積分  (3)

を変数を変えて計算する：

が単射なら int_Uf(g(u)) TemplateBox[{TemplateBox[{{{(, {partial, g}, )}, /, {(, {partial, u}, )}}}, Det]}, Abs]du=int_(g(U))f(v)dv である：

積分の境界を決定するために の範囲を求める：

積分を計算する：

もとの積分を直接計算する：

半径 の球体の表面積を有理パラメータ化を使って計算する：

パラメータ化が単射であることを確認する：

表面積は，のグラム(Gram)行列式の平方根の積分と同じである：

有理パラメータ化を使って を「8の字曲面」上で積分する：

一次元集合の外側でパラメータ化が単射であることを確認する：

g(f(t,u))sqrt(TemplateBox[{{TemplateBox[{{(, {{(, {partial, f}, )}, /, {(, {partial, {{, {t, ,, u}, }}}, )}}, )}}, Transpose], ., {(, {{(, {partial, f}, )}, /, {(, {partial, {{, {t, ,, u}, }}}, )}}, )}}}, Det])の積分を計算する：

「8の字曲面」の陰的説明を使って計算した値と比較する：

特性と関係  (3)

は，方程式 が各 について最大1つの解を持つときかつそのときに限り単射である：

Solveを使って解を求める：

連結集合上の実数値の一変量連続関数は，単調であるときかつそのときに限り単射である：

FunctionMonotonicityを使って関数の単調性を決定する：

複素多項式写像は，逆多項式を持つときかつそのときに限り単射である：

Solveを使って逆多項式を求める：

が の両側逆元であることを確認する：

考えられる問題  (1)

FunctionInjectiveはFunctionDomainを使って関数の実領域を決定する：

はFunctionDomainが報告した実領域において単射である：

は実数値で実数全体上では単射ではない：

点が の実領域に属するためには， の部分式はすべて実数値でなければならない：

Wolfram Research (2020), FunctionInjective, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionInjective.html.

テキスト

Wolfram Research (2020), FunctionInjective, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionInjective.html.

CMS

Wolfram Language. 2020. "FunctionInjective." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionInjective.html.

APA

Wolfram Language. (2020). FunctionInjective. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionInjective.html

BibTeX

@misc{reference.wolfram_2024_functioninjective, author="Wolfram Research", title="{FunctionInjective}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionInjective.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functioninjective, organization={Wolfram Research}, title={FunctionInjective}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionInjective.html}, note=[Accessed: 21-November-2024 ]}