FunctionInjective
FunctionInjective[f,x]
测试对于每一个 y,![]() 是否最多只有一个解 x∈Reals.
是否最多只有一个解 x∈Reals.
FunctionInjective[f,x,dom]
测试 ![]() 是否最多只有一个解 x∈dom.
是否最多只有一个解 x∈dom.
FunctionInjective[{f1,f2,…},{x1,x2,…},dom]
测试 ![]() 是否最多只有一个解 x1,x2,…∈dom.
是否最多只有一个解 x1,x2,…∈dom.
FunctionInjective[{funs,xcons,ycons},xvars,yvars,dom]
测试对于每一个受约束条件 ycons 限制的 yvars∈dom,![]() 是否最多只有一个受约束条件 xcons 限制的解 xvars∈dom.
是否最多只有一个受约束条件 xcons 限制的解 xvars∈dom.
更多信息和选项

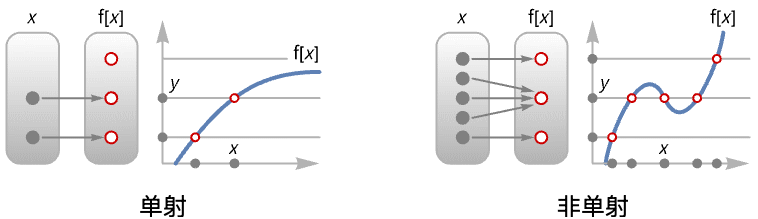
- 单射函数也被称为一一映射 (one-to-one).
- 如果对于每个
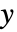 ,最多存在一个
,最多存在一个 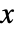 ,使得
,使得 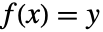 ,则函数
,则函数 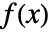 是单射的.
是单射的. - 如果映射
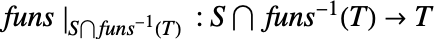 是单射,则 FunctionInjective[{funs,xcons,ycons},xvars,yvars,dom] 返回 True,其中
是单射,则 FunctionInjective[{funs,xcons,ycons},xvars,yvars,dom] 返回 True,其中 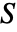 是 xcons 的解集,
是 xcons 的解集,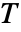 是 ycons 的解集.
是 ycons 的解集. - 如果 funs 含有除 xvars 之外的参数,则结果通常为 ConditionalExpression.
- dom 的可能的值为 Reals 和 Complexes. 如果 dom 是 Reals,则所有变量、参数、常数和函数值都必须为实数.
- funs 的定义域受 FunctionDomain 给定的条件限制.
- xcons 和 ycons 可含有等式、不等式或它们的逻辑组合.
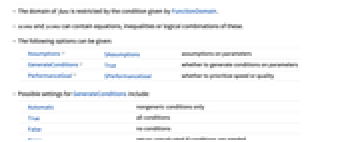
- 可给出以下选项:
-
Assumptions $Assumptions 对参数的设定 GenerateConditions True 是否生成关于参数的条件 PerformanceGoal $PerformanceGoal 优先考虑速度还是质量 - GenerateConditions 的可能的设置包括:
-
Automatic 只给出非通用条件 True 给出所有条件 False 不给出条件 None 如果需要条件则不经计算直接返回 - PerformanceGoal 的可能设置为 "Speed" 和 "Quality".
范例
打开所有单元关闭所有单元选项 (4)
Assumptions (1)
FunctionInjective 无法确定 ![]() 取任意值时
取任意值时 ![]() 的单射性:
的单射性:
如果假设 ![]() 为奇整数,FunctionInjective 即可确定函数的单射性:
为奇整数,FunctionInjective 即可确定函数的单射性:
GenerateConditions (2)
默认情况下,FunctionInjective 可能会对符号参数生成条件:
如果设置 GenerateConditionsNone,FunctionInjective 会失败,而不是给出有条件的结果:
如果设置 GenerateConditionsAutomatic,不报告通常为真的条件:
PerformanceGoal (1)
用 PerformanceGoal 避免潜在费时的计算:
应用 (17)
基本应用 (8)
查看 Clip[x] 在所有实数上的单射性:
![]() 和
和 ![]() 在 [-∞,-1] 和 [1, ∞] 上被取了不止一次:
在 [-∞,-1] 和 [1, ∞] 上被取了不止一次:
限制在区间 [-1, 1] 上的 Clip[x] 是单射的:
用 FunctionPeriod 查看函数是否是周期函数:
用 FunctionSign 求导数的正负性:
部分 ParametricPlot 被覆盖了两次:
ParametricPlot 的每个点只被覆盖了一次:
解方程与不等式 (4)
概率与统计 (2)
属性和关系 (3)
用 Solve 求出解:
用 FunctionMonotonicity 确定函数的单调性:
当且仅当复多项式映射有多项式逆元 (polynomial inverse),它才是单射的:
用 Solve 求多项式的逆元:
可能存在的问题 (1)
FunctionInjective 用 FunctionDomain 确定函数的实定义域:
在 FunctionDomain 给出的实定义域上,![]() 是单射的:
是单射的:
文本
Wolfram Research (2020),FunctionInjective,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FunctionInjective.html.
CMS
Wolfram 语言. 2020. "FunctionInjective." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionInjective.html.
APA
Wolfram 语言. (2020). FunctionInjective. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FunctionInjective.html 年