GibbsPointProcess
GibbsPointProcess[{"PairPotential",μ, ϕ}, d]
![]() における,密度 μ,対ポテンシャル関数 ϕ のGibbs点過程を表す.
における,密度 μ,対ポテンシャル関数 ϕ のGibbs点過程を表す.
GibbsPointProcess[{"PairInteraction",μ, h}, d]
![]() における,密度 μ,対相互作用 h のGibbs点過程を表す.
における,密度 μ,対相互作用 h のGibbs点過程を表す.
GibbsPointProcess[{"Papangelou",λ*}, d]
![]() における,Papangelou条件密度
における,Papangelou条件密度 ![]() のGibbs点過程を表す.
のGibbs点過程を表す.
GibbsPointProcess[{"Density",f}, d]
![]() における,密度関数が f に比例するGibbs点過程を表す.
における,密度関数が f に比例するGibbs点過程を表す.
詳細

- GibbsPointProcessはマルコフ(Markov)点過程としても知られている.
- Gibbsモデルは,一般に,資源を競う木や植物や,互いに反発したり引き付けたりする粒子のような,点と点の相互作用のモデル化に使われる.
- 点のペアの間の相互作用だけを持つGibbs点過程は,その密度関数
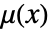 とラジアル対ポテンシャル関数
とラジアル対ポテンシャル関数 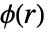 あるいは対相互作用関数
あるいは対相互作用関数 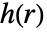 によって指定することができる.
によって指定することができる. - 密度関数
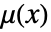 は位置が
は位置が 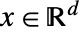 の非負の関数で,点の相互作用が存在しない場合は
の非負の関数で,点の相互作用が存在しない場合は 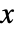 の近傍の点の期待数をモデル化する.
の近傍の点の期待数をモデル化する. - 対ポテンシャル関数
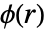 は点と点の間の距離の実数関数である.
は点と点の間の距離の実数関数である.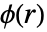 の値が高くなる程,お互いに距離
の値が高くなる程,お互いに距離 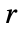 にある2つの点が存在する可能性が低くなることを意味する.
にある2つの点が存在する可能性が低くなることを意味する. - 対相互作用関数
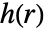 は,
は,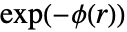 で与えられるもので,点と点の間の距離を表す非負の関数である.
で与えられるもので,点と点の間の距離を表す非負の関数である.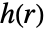 の値が高くなる程,お互いに距離
の値が高くなる程,お互いに距離 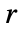 にある2つの点が存在する可能性が高くなることを意味する.
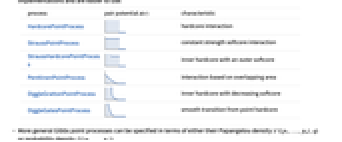
にある2つの点が存在する可能性が高くなることを意味する. - GibbsPointProcessはGibbs点過程を表すことができる.一般的なGibbs過程には専用の実装があり,使いやすくなっている.
-
過程 対ポテンシャル 
特徴 HardcorePointProcess 
ハードコア相互作用 StraussPointProcess 
一定の強さのソフトコア相互作用 StraussHardcorePointProcess 
外側がソフトコアで内側がハードコア PenttinenPointProcess 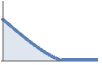
重なり合う部分に基づいた相互作用 DiggleGrattonPointProcess 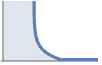
内側がハードコアで減少するソフトコア DiggleGatesPointProcess 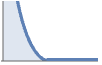
点ハードコアからの滑らかな変化 - より一般的なGibbs点過程は,Papangelou密度
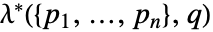 か確率密度
か確率密度  によって指定できる.
によって指定できる. - Papangelou密度
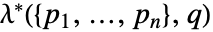 は点
は点 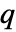 を点の集合
を点の集合 に加えるコストを指定するもので,非負の関数でなければならない.
に加えるコストを指定するもので,非負の関数でなければならない. - 密度
 は点配置の確率密度を指定する.関数 f は非負でなければならないが,正規化されている必要はない.
は点配置の確率密度を指定する.関数 f は非負でなければならないが,正規化されている必要はない. - GibbsPointProcessでは,d は任意の正の整数でよい.
- すべての指定が以下で与えられるものと同等のPapangelou密度 λ*を持つ.
-
{"PairPotential",μ,ϕ} ![mu exp(-sum_iphi(TemplateBox[{{{p, _, i}, -, q}}, Norm])) mu exp(-sum_iphi(TemplateBox[{{{p, _, i}, -, q}}, Norm]))](Files/GibbsPointProcess.ja/32.png)
{"PairInteraction",μ,h} ![mu product_ip(TemplateBox[{{{p, _, i}, -, q}}, Norm]) mu product_ip(TemplateBox[{{{p, _, i}, -, q}}, Norm])](Files/GibbsPointProcess.ja/33.png) .
.{"Density",f} 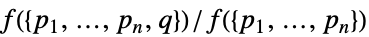
- GibbsPointProcessは,RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる.
例題
すべて開くすべて閉じる例 (1)
適切な密度関数を持つGibbsPointProcessでポアソン点過程からサンプルを取る:
スコープ (4)
密度が点の数に比例するGibbs点過程のシミュレーションを行う:
マルコフ鎖モンテカルロ法を使って単位円板上で40個のサンプルのシミュレーションを行う:
GibbsPointProcessでStrauss点過程からサンプルを取る:
Papangelou条件密度を指定して同じ過程からサンプルを取る:
密度![]() のポアソン点過程について半径0.3のハードコア点過程からサンプルを取る:
のポアソン点過程について半径0.3のハードコア点過程からサンプルを取る:
StraussHardcorePointProcessのように単純なGibbs点過程は,強度 ![]() と対ポテンシャル
と対ポテンシャル ![]() だけによって 表現される密度を持つが,これは一般的には真ではない.点の周りの円板の共通集合の面積に依存する点過程は,以下の密度関数が示すように,点の可能なすべての部分集合に依存する相互作用を持つ:
だけによって 表現される密度を持つが,これは一般的には真ではない.点の周りの円板の共通集合の面積に依存する点過程は,以下の密度関数が示すように,点の可能なすべての部分集合に依存する相互作用を持つ:
特性と関係 (1)
PoissonPointProcessとGibbsPointProcessから適切な密度で生成された点の数を比較する:
テキスト
Wolfram Research (2020), GibbsPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/GibbsPointProcess.html.
CMS
Wolfram Language. 2020. "GibbsPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GibbsPointProcess.html.
APA
Wolfram Language. (2020). GibbsPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GibbsPointProcess.html