StraussPointProcess[μ,γ,rs,d]
represents a Strauss point process with constant intensity μ, interaction parameter γ and interaction radius rs in d.


StraussPointProcess
StraussPointProcess[μ,γ,rs,d]
represents a Strauss point process with constant intensity μ, interaction parameter γ and interaction radius rs in d.
Details


- StraussPointProcess models point configurations with a constant repulsive pairwise interaction for points within radius rs of each other but that are otherwise uniformly distributed.
- The Strauss model is typically used when the process interaction has a constant penalty for points within radius rs, including for locations of plants, birds nests and biological cells.
-
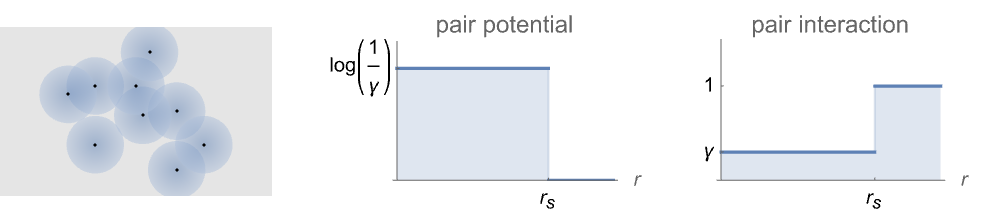
- The Strauss point process can be defined as a GibbsPointProcess in terms of its intensity μ and the pair potential ϕ or pair interaction h, which are both parametrized by γ and rs as follows:
-
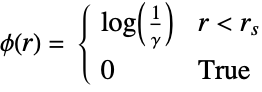
pair potential 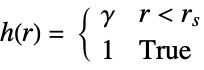
pair interaction - A point configuration
 from a Strauss point process StraussPointProcess[μ,γ,rs,d] in an observation region reg has density function
from a Strauss point process StraussPointProcess[μ,γ,rs,d] in an observation region reg has density function  proportional to
proportional to 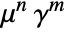 , where
, where ![m=sum_(i!=j)Boole[TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]<r_s] m=sum_(i!=j)Boole[TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]<r_s]](Files/StraussPointProcess.en/7.png) with respect to PoissonPointProcess[1,d].
with respect to PoissonPointProcess[1,d]. - The Papangelou conditional density
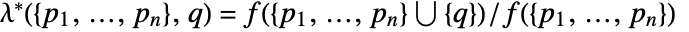 for adding a point
for adding a point 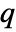 to a point configuration
to a point configuration  is
is 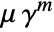 where
where ![m=sum_iBoole[TemplateBox[{{{p, _, i}, -, q}}, Norm]<r_s] m=sum_iBoole[TemplateBox[{{{p, _, i}, -, q}}, Norm]<r_s]](Files/StraussPointProcess.en/12.png) .
. - StraussPointProcess allows μ, γ and
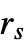 to be any positive numbers such that
to be any positive numbers such that 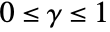 , and d to be any positive integer.
, and d to be any positive integer. - StraussPointProcess simplifies to HardcorePointProcess when
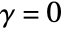 and to PoissonPointProcess when
and to PoissonPointProcess when 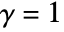 . Smaller values of
. Smaller values of 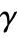 inhibit points being closer than
inhibit points being closer than 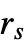 .
. - Possible Method settings in RandomPointConfiguration for StraussPointProcess are:
-
"MCMC" Markov chain Monte Carlo birth and death "Exact" coupling from the past - Possible PointProcessEstimator settings in EstimatedPointProcess for StraussPointProcess are:
-
Automatic automatically choose the parameter estimator "MaximumPseudoLikelihood" maximize the pseudo-likelihood - StraussPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.
Examples
open all close allBasic Examples (2)
Scope (4)
Options (4)
Possible Issues (2)
By default, the simulation will run until the number of points converges to a steady state, or until the default number of iterations is reached:
Raise the number of recursive calls to the sampler:
Specify a larger length of run:
The objective function for estimating the parameters is the pseudo log-likelihood:
Related Guides
History
Text
Wolfram Research (2020), StraussPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/StraussPointProcess.html.
CMS
Wolfram Language. 2020. "StraussPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StraussPointProcess.html.
APA
Wolfram Language. (2020). StraussPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StraussPointProcess.html
BibTeX
@misc{reference.wolfram_2025_strausspointprocess, author="Wolfram Research", title="{StraussPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/StraussPointProcess.html}", note=[Accessed: 21-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_strausspointprocess, organization={Wolfram Research}, title={StraussPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/StraussPointProcess.html}, note=[Accessed: 21-January-2026]}