RandomPointConfiguration[pproc,reg]
generates a pseudorandom spatial point configuration from the spatial point process pproc in the observation region reg.
RandomPointConfiguration[pproc,reg, n]
generates an ensemble of n spatial point configurations.


RandomPointConfiguration
RandomPointConfiguration[pproc,reg]
generates a pseudorandom spatial point configuration from the spatial point process pproc in the observation region reg.
RandomPointConfiguration[pproc,reg, n]
generates an ensemble of n spatial point configurations.
Details and Options

- RandomPointConfiguration takes a point process pproc and generates a point configuration as a SpatialPointData object.
- RandomPointConfiguration gives a different realization of pseudorandom point configurations whenever you run the Wolfram Language. You can start with a particular seed using SeedRandom.
- The same process can generate an ensemble consisting of different realizations.
- The observation region reg needs to be a parameter-free region, as well as SpatialObservationRegionQ.
- The following options can be given:
-
Method Automatic what method to use WorkingPrecision MachinePrecision precision used in internal computations - With the setting WorkingPrecisionp, random numbers of precision p will be generated.
- Special settings for Method are documented under the individual point process reference pages.
- Typical Method settings include:
-
"MCMC" Markov chain Monte Carlo birth and death "Thinning" random thinning "Exact" coupling from the past
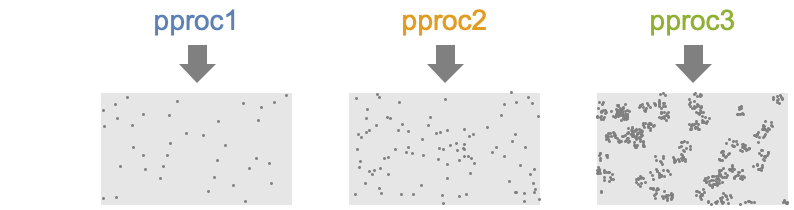

Examples
open all close allBasic Examples (3)
Scope (5)
RandomPointConfiguration returns a SpatialPointData object:
Obtain a list of locations of the points:
Simulate a Strauss point process in a rectangle:
Retrieve points that lie within a unit disk centered at {2,3}:
Visualize points on the plane:
Estimate the parameters for a point process using a simulated point configuration:
Simulate from a Cauchy point process:
Estimate Ripley's ![]() function from the sampled point configuration and compare it with the theoretical
function from the sampled point configuration and compare it with the theoretical ![]() function:
function:
Simulate an ensemble of 5 realizations over the same region:
Number of points in each realization:
Visualize the distribution of points in different realizations:
Options (3)
Method (2)
Sample from an InhomogeneousPoissonPointProcess using the different methods:
Use the Markov chain Monte Carlo method "MCMC":
Visualize samples over the region:
Sample from a Gibbs point process using the Markov chain Monte Carlo method "MCMC" with the number of iterations equal to 30000:
WorkingPrecision (1)
Generate a sample point configuration with default machine precision:
Use WorkingPrecision to generate a sample point configuration with higher precision:
Applications (2)
Estimate the density of a PoissonPointProcess from a sample:
Compare the expected point counts and the average of number of points for an inhomogeneous Poisson point process:
Related Guides
History
Text
Wolfram Research (2020), RandomPointConfiguration, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPointConfiguration.html.
CMS
Wolfram Language. 2020. "RandomPointConfiguration." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPointConfiguration.html.
APA
Wolfram Language. (2020). RandomPointConfiguration. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPointConfiguration.html
BibTeX
@misc{reference.wolfram_2025_randompointconfiguration, author="Wolfram Research", title="{RandomPointConfiguration}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPointConfiguration.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_randompointconfiguration, organization={Wolfram Research}, title={RandomPointConfiguration}, year={2020}, url={https://reference.wolfram.com/language/ref/RandomPointConfiguration.html}, note=[Accessed: 25-February-2026]}