PoissonPointProcess[μ,d]
represents a homogeneous Poisson point process with constant intensity μ in ![]() .
.


PoissonPointProcess
PoissonPointProcess[μ,d]
represents a homogeneous Poisson point process with constant intensity μ in ![]() .
.
Details

- PoissonPointProcess is also known as homogeneous Poisson point process, stationary Poisson point process and complete spatial randomness (CSR).
- PoissonPointProcess generates points that are uniformly distributed in a region, with the average number of points per unit volume equal to μ.
- Typical uses are to model and test point collections that are completely spatially random. They are frequently used as building blocks for more complicated point processes such as clustered point processes.
- With intensity μ, the number of points in the observation region with volume
 follows the distribution PoissonDistribution[μ ν].
follows the distribution PoissonDistribution[μ ν]. - The number of points
 in disjoint regions
in disjoint regions 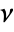 for a Poisson point process consists of independent random variables so
for a Poisson point process consists of independent random variables so 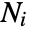 . This property is also referred to as complete spatial randomness (CSR).
. This property is also referred to as complete spatial randomness (CSR). - A point configuration
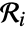 with intensity μ in an observation region
with intensity μ in an observation region 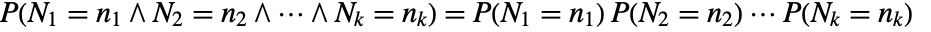 with volume
with volume  has density function
has density function 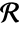 with respect to PoissonPointProcess[1,d].
with respect to PoissonPointProcess[1,d]. - The Papangelou conditional density
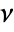 for adding a point
for adding a point 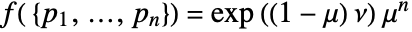 to a point configuration
to a point configuration 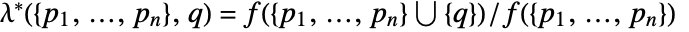 is
is 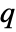 for a Poisson point process with intensity μ.
for a Poisson point process with intensity μ. - PoissonPointProcess allows μ to be any positive real number and d to be any positive integer.
- Possible PointProcessEstimator settings in EstimatedPointProcess for PoissonPointProcess are:
-
Automatic automatically choose the parameter estimator "MaximumPseudoLikelihood" maximize the pseudo-likelihood - PoissonPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.

Examples
open all close allBasic Examples (3)
Scope (4)
Sample a Poisson point process from any valid region whose RegionEmbeddingDimension is equal to its RegionDimension:
Sample points from the region:
Sample from PoissonPointProcess using the different methods:
Use Markov chain Monte Carlo method:
Estimate PoissonPointProcess:
Estimate PoissonPointProcess over a geo region:
Find PointCountDistribution:
Applications (3)
Suppose flaws in plywood occur on an average of one flaw per 50 square feet. Simulate the process of finding flaws on a per-square-foot basis:
Find the probability that a 4-foot×8-foot sheet will have no flaws:
For a round mirror with area 7.54 cm![]() , the probability of no flaws is 0.91. Using the same polishing process, another round mirror with an area of 19.50 cm
, the probability of no flaws is 0.91. Using the same polishing process, another round mirror with an area of 19.50 cm![]() is fabricated. Assuming the flaws are independent and randomly located, find the probability of no flaws on the larger mirror:
is fabricated. Assuming the flaws are independent and randomly located, find the probability of no flaws on the larger mirror:
Find the intensity of the flaw point process:
The resulting mirror polishing defect process is then:
The probability of no errors in the larger mirror:
An LCD display has 1920×1080 pixels. A display is accepted if it has 15 or fewer faulty pixels. The probability that a pixel is faulty from production is ![]() and the faulty pixel positions are independent and random. Find the proportion of displays that are accepted:
and the faulty pixel positions are independent and random. Find the proportion of displays that are accepted:
Simulate the faulty pixel configuration:
Find the probability of no more than 15 faulty pixels in the display:
Find the pixel failure rate required to produce 4000×2000 pixel displays and still have an acceptance rate of at least 90%:
Plot the acceptance rate as a function of the pixel failure rate:
Find the maximal acceptable pixel failure rate:
Properties & Relations (11)
The number of points in a PoissonPointProcess is Poisson distributed:
Simulate a PoissonPointProcess over a unit disk:
Compare the histogram of point counts with the PDF:
Fit a PoissonDistribution to the point counts:
Test against the underlying distribution:
Compute void probabilities for a Poisson point process. For a disk:
The probability of finding a point within distance ![]() of an arbitrary location:
of an arbitrary location:
This equivalent to the CDF of RayleighDistribution:
Equivalently compute SurvivalFunction at 0 of PointCountDistribution:
Poisson point process is stationary—the intensity is translation invariant:
Point count distribution in a subregion:
Point count distribution in the translated subregion:
Poisson point process is isotropic—the intensity is rotation around origin invariant:
Point count distribution in a subregion:
Point count distribution in the translated subregion:
PoissonPointProcess has the property of complete spatial randomness:
Define left and right half-disks:
Create subset of points in each subregion:
Extract the number of points for each subregion:
Test whether two samples are independent:
Ripley's ![]() function for the Poisson point process has closed form and does not depend on the intensity:
function for the Poisson point process has closed form and does not depend on the intensity:
Plot the function for few dimensions:
Besag's ![]() for the Poisson point process does not depend on intensity or dimensionality:
for the Poisson point process does not depend on intensity or dimensionality:
PairCorrelationG for the Poisson point process is constant:
EmptySpaceF and NearestNeighborG functions of a Poisson point process are identical:
They both are equivalent to the CDF of an ExponentialDistribution:
InhomogeneousPoissonPointProcess with a constant intensity function is PoissonPointProcess:
The point count distribution in a disk:
Point count distribution for a corresponding Poisson point process in the same region:
The point count distribution in a ball:
Point count distribution for a corresponding Poisson point process in the same region:
Related Guides
History
Text
Wolfram Research (2020), PoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PoissonPointProcess.html.
CMS
Wolfram Language. 2020. "PoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonPointProcess.html.
APA
Wolfram Language. (2020). PoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PoissonPointProcess.html
BibTeX
@misc{reference.wolfram_2025_poissonpointprocess, author="Wolfram Research", title="{PoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PoissonPointProcess.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_poissonpointprocess, organization={Wolfram Research}, title={PoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/PoissonPointProcess.html}, note=[Accessed: 09-March-2026]}