InhomogeneousPoissonProcess[λ[t],t]
represents an inhomogeneous Poisson process with intensity λ[t] given as a function of t.


InhomogeneousPoissonProcess
InhomogeneousPoissonProcess[λ[t],t]
represents an inhomogeneous Poisson process with intensity λ[t] given as a function of t.
Details
- InhomogeneousPoissonProcess is a continuous-time and discrete-state process.
- InhomogeneousPoissonProcess at time t is the number of events in the interval 0 to t.
- The number of events in the interval 0 to t follows PoissonDistribution with mean
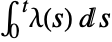 .
. - The intensity function λ[t] in the definition of InhomogeneousPoissonProcess is assumed to be valid. In particular, it is assumed that it is a continuous, positive-valued function of t.
- InhomogeneousPoissonProcess can be used with such functions as Mean, PDF, Probability, and RandomFunction.
Examples
open all close allBasic Examples (3)
Scope (10)
Basic Uses (5)
Process Slice Properties (5)
Univariate SliceDistribution:
Univariate probability density:
Multi-time slice distribution:
Higher-order PDF:
Compute the expectation of an expression:
Calculate the probability of an event:
CentralMoment has no closed form for symbolic order:
FactorialMoment and its generating function:
Cumulant and its generating function:
Applications (3)
Simulate the arrival process at a small fast-food restaurant if the hourly arrival rates of customers are given by:
Use linear interpolation to obtain the intensity function for the arrival process:
Define an inhomogeneous Poisson process for the arrivals:
Probability that more than 200 customers visit the restaurant during the day:
Simulate the arrival process for a day:
Use simulation to find the effective hourly mean arrival rate:
Define the square of an inhomogeneous Poisson process:
Mean and variance for the process slices:
An inhomogeneous Poisson process with Weibull failure rate intensity is known as Weibull Poisson process:
Use simulation to find the effective mean intensity rate for a day:
Compare to the mean intensity rate given by the integral of the rate function:
Properties & Relations (3)
InhomogeneousPoissonProcess is a jump process:
An inhomogeneous Poisson process is not weakly stationary:
The mean function is not constant:
An inhomogeneous Poisson process with constant intensity is a PoissonProcess:
Possible Issues (1)
Related Guides
History
Text
Wolfram Research (2015), InhomogeneousPoissonProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
CMS
Wolfram Language. 2015. "InhomogeneousPoissonProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html.
APA
Wolfram Language. (2015). InhomogeneousPoissonProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html
BibTeX
@misc{reference.wolfram_2025_inhomogeneouspoissonprocess, author="Wolfram Research", title="{InhomogeneousPoissonProcess}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inhomogeneouspoissonprocess, organization={Wolfram Research}, title={InhomogeneousPoissonProcess}, year={2015}, url={https://reference.wolfram.com/language/ref/InhomogeneousPoissonProcess.html}, note=[Accessed: 06-January-2026]}