InhomogeneousPoissonPointProcess

InhomogeneousPoissonPointProcess[μ,d]

represents an inhomogeneous Poisson point process with density function in .

Details

  • InhomogeneousPoissonPointProcess is also known as a nonstationary Poisson point process or an independent scattering point process.
  • Typical uses include modeling varying density that depends only on the location 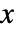, such as varying growth conditions.
  • InhomogeneousPoissonPointProcess generates points in a region according to the specified density function μ with no point interactions.
  • With density function μ, the point count in an observation region is distributed as PoissonDistribution with mean .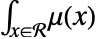
  • Density function μ can be given as:
  • funca function of vectors
    geofunca function of geo locations
    PointDensityFunctiondensity function from point collections
  • The number of points in disjoint regions 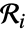for a Poisson point process are independent 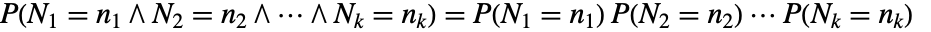, where 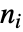are non-negative integers.
  • A point configuration with density function μ in an observation region 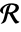with volume has density function with respect to PoissonPointProcess[1,d].
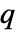  • The Papangelou conditional density for adding a point to a point configuration is 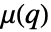for an inhomogeneous Poisson point process with density function μ.
  • The density function 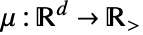can be any positive integrable function in 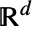and d can be any positive integer.
  • InhomogeneousPoissonPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.

Examples

open allclose all

Basic Examples  (4)

Sample from an InhomogeneousPoissonPointProcess:

Sample from an InhomogeneousPoissonPointProcess defined on the surface of the Earth:

Visualize the points:

Sample from a nonparametric point density:

Sample from a binned density:

Define a point process with the computed point density function and check if it is valid:

Simulate multiple point configurations:

Scope  (4)

Simulate several realizations:

Sample from any valid RegionQ, whose RegionEmbeddingDimension is equal to its RegionDimension:

Check the region conditions:

Sample points:

Gaussian scattering is an example of isotropic inhomogeneous Poisson point process:

Simulate the process over a rectangle:

PointCountDistribution is invariant with respect to a rotation about the origin:

Point count distribution in the rotated region:

The distributions are the same as identified by equal means:

Define piecewise density:

Define process:

Sample from the process:

Options  (1)

Method  (1)

Sample from an InhomogeneousPoissonPointProcess using different methods:

Use the thinning method:

Use the Markov chain Monte Carlo method:

Plot samples over the region:

Applications  (2)

Point process with density depending on the distance to a line, like a fault line:

Define the point process:

Simulate the process:

Simulate possible point pattern of seeds fallen around a tree:

Define the point process:

Simulate the process:

Simulate the seed pattern:

Properties & Relations  (5)

Inhomogeneous Poisson point process with constant density autoevaluates to PoissonPointProcess:

The expected number of points in a region for InhomogeneousPoissonPointProcess follows a PoissonDistribution:

Compute the point count distribution over a rectangle:

Over a disk:

Over an implicit region:

Compute void probabilities for an inhomogeneous Poisson point process:

For a rectangle:

For the rectangle translated:

Inhomogeneous Poisson point process is not stationary—the density depends on the location:

Point count distribution in a subregion:

Point count distribution in the translated subregion:

The region measures are the same:

The densities as expressed via PointCountDistribution differ:

InhomogeneousPoissonPointProcess with a constant density function is PoissonPointProcess:

The point count distribution in a disk:

Point count distribution for a corresponding Poisson point process in the same region:

In higher dimension:

The point count distribution in a ball:

Point count distribution for a corresponding Poisson point process in the same region:

Neat Examples  (1)

Use region-dependent density:

Wolfram Research (2020), InhomogeneousPoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

Text

Wolfram Research (2020), InhomogeneousPoissonPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

CMS

Wolfram Language. 2020. "InhomogeneousPoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

APA

Wolfram Language. (2020). InhomogeneousPoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html

BibTeX

@misc{reference.wolfram_2025_inhomogeneouspoissonpointprocess, author="Wolfram Research", title="{InhomogeneousPoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_inhomogeneouspoissonpointprocess, organization={Wolfram Research}, title={InhomogeneousPoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html}, note=[Accessed: 21-February-2025 ]}