SmoothPointDensity

SmoothPointDensity[pdata]

estimates the point density function for point data pdata.

SmoothPointDensity[pdata,bw]

estimates the density for point data pdata with bandwidth bw.

SmoothPointDensity[pdata,bw,ker]

estimates the density for point data pdata with bandwidth bw and smoothing kernel ker.

SmoothPointDensity[bdata,…]

estimates the point density function for binned data bdata.

SmoothPointDensity[pproc,…]

computes the density function for point process pproc.

Details and Options

  • Point density is also known as point intensity.
  • SmoothPointDensity gives a function 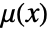that describes how the number of points 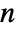varies per length, area and volume in the observation region 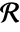. The integral over the region is the total number of points .
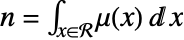  • SmoothPointDensity is a kernel-based estimator of the point density, where bandwidth bw and kernel ker are used to control the smoothing.
  • SmoothPointDensity returns a PointDensityFunction that can be used to evaluate the density function repeatedly.
  • The points pdata can have the following forms:
  • {p1,p2,…}points pi
    GeoPosition[…],GeoPositionXYZ[…],…geographic points
    SpatialPointData[…]spatial point collection
    {pts,reg}point collection pts and observation region reg
  • If the observation region reg is not given, a region is automatically computed using RipleyRassonRegion.
  • The point process pproc can have the following forms:
  • proca point process proc
    {proc,reg}a point process proc and observation region reg
  • The observation region reg should be a parameter-free, full-dimensional and bounded region as tested by SpatialObservationRegionQ.
  • With a point process pproc, either exact formulas or approximate computation methods are used.
  • The following bandwidth specifications bw can be given:
  • hbandwidth to use
    {"Standardized",h}bandwidth in units of standard deviations
    {"Adaptive",h,s}adaptive with initial bandwidth h and sensitivity s
    Automaticautomatically computed bandwidth
    "name"use a named bandwidth selection method
    {bwx,bwy,…}separate bandwidth specifications for x, y, etc.
  • For multivariate densities, h can be a positive definite symmetric matrix.
  • For adaptive bandwidths, the sensitivity s must be a real number between 0 and 1 or Automatic. If Automatic is used, s is set to 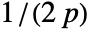, where 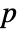is the dimensionality of the data.
  • Possible named bandwidth selection methods include:
  • "LeastSquaresCrossValidation"use the method of least-squares cross-validation
    "Oversmooth"1.08 times wider than the standard Gaussian
    "Scott"use Scott's rule to determine bandwidth
    "SheatherJones"use the Sheather–Jones plugin estimator
    "Silverman"use Silverman's rule to determine bandwidth
    "StandardDeviation"use the standard deviation as bandwidth
    "StandardGaussian"optimal bandwidth for standard normal data
  • By default, the "Silverman" method is used.
  • For automatic bandwidth computation, constant arrays are assumed to have unit variance.
  • The following kernel specifications ker can be given:
  • "Biweight"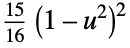
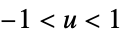
    "Cosine"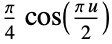
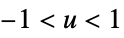
    "Epanechnikov"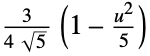
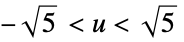
    "Gaussian"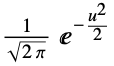
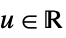
    "Rectangular"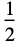
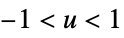
    "SemiCircle"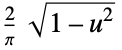
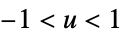
    "Triangular"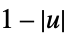
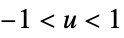
    "Triweight"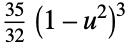
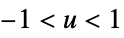
    funcf_nu in R
  • By default, the "Gaussian" kernel is used.
  • For multivariate densities, the kernel function ker can be specified as product and radial types using {"Product",ker} and {"Radial",ker}, respectively. Product-type kernels are used if no type is specified.
  • The precision used for density estimation is the minimum precision given in the bw and data.
  • The following option can be given:
  • Method Automaticthe method to use in the estimation
  • Possible settings for Method are Automatic, "KernelMixture", "SmoothKernel".
  • Possible suboptions for "KernelMixture" method:
  • MaxMixtureKernelsAutomaticmax number of kernels to use
  • Possible suboptions for "SmoothKernel" method:
  • InterpolationPointsAutomaticinitial number of interpolation points to use
    MaxMixtureKernelsAutomaticmax number of kernels to use
    MaxRecursionAutomaticnumber of recursive subdivisions to allow
    PerformanceGoalAutomaticoptimize for speed or quality
    MaxExtraBandwidthsAutomaticmax bandwidths beyond data to use

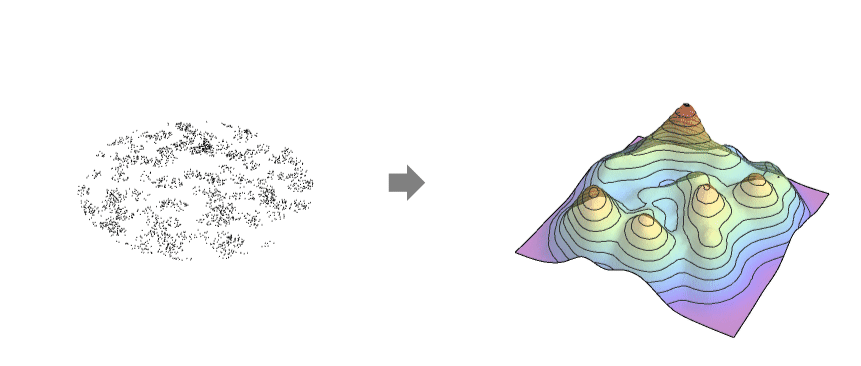
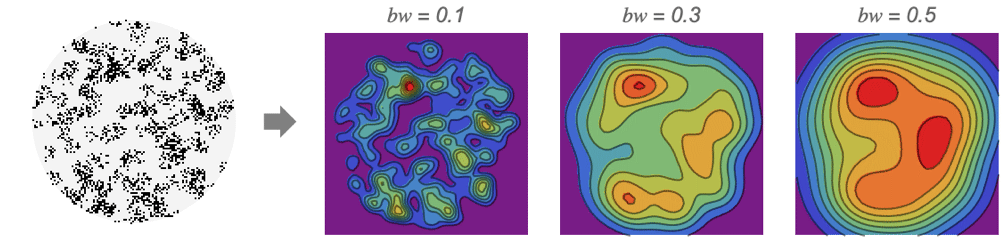
Examples

open allclose all

Basic Examples  (1)

Create a SpatialPointData:

Plot the points:

Estimate the point density:

Value at a point:

Visualize the density estimation:

Scope  (4)

Create a homogeneous univariate SpatialPointData:

Compute point density function using kernel mixture:

Confirm the type:

Visualize:

Create an inhomogeneous univariate SpatialPointData:

Compute the smooth kernel density:

Confirm the type:

Visualize:

Compute smooth point density of clustered data:

Compute smooth point density from data:

Visualize the density function with data points:

Compute smooth point density for a hardcore point process sample:

Compute smooth point density for various bandwidths:

Visualize:

Options  (1)

Method  (1)

Compare methods for computing smooth point density:

Plot the points:

Estimate the point density:

Neat Examples  (1)

Smooth point density of a cluster point process:

Wolfram Research (2020), SmoothPointDensity, Wolfram Language function, https://reference.wolfram.com/language/ref/SmoothPointDensity.html.

Text

Wolfram Research (2020), SmoothPointDensity, Wolfram Language function, https://reference.wolfram.com/language/ref/SmoothPointDensity.html.

CMS

Wolfram Language. 2020. "SmoothPointDensity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SmoothPointDensity.html.

APA

Wolfram Language. (2020). SmoothPointDensity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SmoothPointDensity.html

BibTeX

@misc{reference.wolfram_2023_smoothpointdensity, author="Wolfram Research", title="{SmoothPointDensity}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SmoothPointDensity.html}", note=[Accessed: 19-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2023_smoothpointdensity, organization={Wolfram Research}, title={SmoothPointDensity}, year={2020}, url={https://reference.wolfram.com/language/ref/SmoothPointDensity.html}, note=[Accessed: 19-April-2024 ]}