Glaisher

Glaisher

グレシャーの定数で数値はである．

詳細

  • NumericQには数値として扱われ，Dには定数として扱われる数学定数である．
  • Glaisherは，Nを使って任意精度で評価することができる．
  • グレシャー(Glaisher)の定数 Aは，を満足する．ただし はリーマンのゼータ関数であるものとする．

予備知識

  • Glaisherは，グレシャーの定数 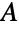を表すシンボルである．これは，グレシャー・キンキリン(Glaisher–Kinkelin)の定数としても知られている．Glaisherの定義は，数学の中でさまざまなものがあるが，もっとも一般的な定義は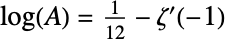，を満足する定数 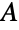である．ただし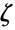， はリーマンのゼータ関数Zetaであり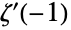，は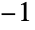で評価されたその導関数，Logは自然対数である．Glaisherは数値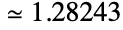を持つ．Glaisherは，総和，積，積分を含む数学計算に見られるが，特にGamma関数およびZeta関数を含む総和と積分に顕著に現れる．
  • Glaisherがシンボルとして使われた場合は，厳密値として伝播される．Glaisherを含む複雑な式の展開と簡約には，FunctionExpand，FullSimplify等の関数が必要な場合がある．
  • Glaisherが，有理数（整数の比で表せる）かどうか，代数的数（整数多項式の根である）かどうか，あるいは任意の底について正規数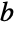（ を底とした展開における数字が一様に分布している）かどうかは，現在のところ判明していない．
  • Glaisherは，Nを使って任意の数値精度に評価することができる．しかし，現在のところ，その桁数が大きい場合の計算のための有効な式は不明である．RealDigitsを使ってGlaisherの各桁の数字を返すことができ，ContinuedFractionを使ってその連分数展開における項を得ることができる．

例題

すべて開くすべて閉じる

例  (1)

任意精度で評価する：

スコープ  (2)

厳密な数値計算を行う：

TraditionalFormによる表示：

アプリケーション  (5)

ゼータ関数の導関数：

ガンマ関数を含む積分：

無限積からGlaisherを得る：

無限和からGlaisherを得る：

極限からGlaisherを得る：

特性と関係  (1)

さまざまな記号的関係が自動的に使われる：

おもしろい例題  (1)

連分数の項：

Wolfram Research (1999), Glaisher, Wolfram言語関数， https://reference.wolfram.com/language/ref/Glaisher.html （2007年に更新）.

テキスト

Wolfram Research (1999), Glaisher, Wolfram言語関数， https://reference.wolfram.com/language/ref/Glaisher.html （2007年に更新）.

CMS

Wolfram Language. 1999. "Glaisher." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Glaisher.html.

APA

Wolfram Language. (1999). Glaisher. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Glaisher.html

BibTeX

@misc{reference.wolfram_2024_glaisher, author="Wolfram Research", title="{Glaisher}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Glaisher.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_glaisher, organization={Wolfram Research}, title={Glaisher}, year={2007}, url={https://reference.wolfram.com/language/ref/Glaisher.html}, note=[Accessed: 21-November-2024 ]}