Glaisher
用来给出 Glaisher 常数,其值 ![]() .
.
背景
- Glaisher 是表示 Glaisher 常数
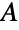 的符号,也被称为 Glaisher–Kinkelin 常数. Glaisher 在数学中有许多等价的定义但最常见的定义还是满足
的符号,也被称为 Glaisher–Kinkelin 常数. Glaisher 在数学中有许多等价的定义但最常见的定义还是满足 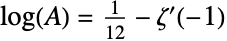 的常数
的常数 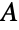 ,其中
,其中 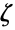 是黎曼 ζ 函数 Zeta,
是黎曼 ζ 函数 Zeta,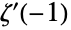 是此函数在
是此函数在 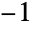 处的导数,而 Log 是自然对数. Glaisher 数值
处的导数,而 Log 是自然对数. Glaisher 数值 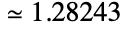 . Glaisher 出现在包括求和、求积以及求积分等各类数学计算中,在涉及 Gamma 和 Zeta 函数的求和与求积中尤为常见.
. Glaisher 出现在包括求和、求积以及求积分等各类数学计算中,在涉及 Gamma 和 Zeta 函数的求和与求积中尤为常见. - 当 Glaisher 作为符号时,它被当成精确值参与计算. 展开及化简一些复杂的含有 Glaisher 的表达式可能要用到如 FunctionExpand 和 FullSimplify 这样的函数.
- 目前不知道 Glaisher 是不是有理数(这意味着它能被表示成一对整数的比值),是不是代数数(这意味着它是某个整数系数多项式的根),是不是某个进位制下的正规数(这意味着它在
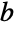 进制下的各位数字均匀分布).
进制下的各位数字均匀分布). - 用 N 可以算出 Glaisher 的任意精度的数值. 然而,目前还不知道能高效计算其大量位数的公式. RealDigits 可用于返回 Glaisher 的各位数字列表而 ContinuedFraction 则可得到其连分数展开的各项.
范例
打开所有单元关闭所有单元范围 (2)
Wolfram Research (1999),Glaisher,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Glaisher.html (更新于 2007 年).
文本
Wolfram Research (1999),Glaisher,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Glaisher.html (更新于 2007 年).
CMS
Wolfram 语言. 1999. "Glaisher." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2007. https://reference.wolfram.com/language/ref/Glaisher.html.
APA
Wolfram 语言. (1999). Glaisher. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Glaisher.html 年