WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

GraphDistanceMatrix[g]

グラフ g 内の頂点間の距離の行列を返す．

GraphDistanceMatrix[g,d]

グラフ g 内で最長距離を d とした頂点間の距離の行列を返す．

GraphDistanceMatrix[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
Method  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
関連するガイド
履歴
引用書式

GraphDistanceMatrix

GraphDistanceMatrix[g]

グラフ g 内の頂点間の距離の行列を返す．

GraphDistanceMatrix[g,d]

グラフ g 内で最長距離を d とした頂点間の距離の行列を返す．

GraphDistanceMatrix[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • GraphDistanceMatrixは最短経路行列としても知られている．
  • GraphDistanceMatrixはSparseArrayオブジェクトか通常の行列を返す．
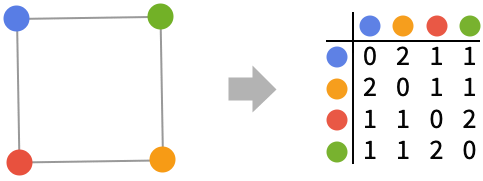
  • 距離行列 dijの項目は頂点 viから頂点 vjまでの最短距離を与える．
  • 距離行列の対角項目 diiは常に0である．
  • 頂点 viから頂点 vjまでの経路が存在しない場合，項目 dijはInfinity(∞)である．
  • GraphDistanceMatrix[g,d]で頂点 viから頂点 vjまでに d ステップ以下の経路が存在しない場合，項目 dijはInfinityになる．
  • 頂点 viはVertexList[g]によって与えられる順序であるとみなされる．
  • 重み付きグラフについては，距離は頂点 viから頂点 vjまでの，任意の経路に沿った重みの和の最低のものである．
  • 使用可能なオプション
  • EdgeWeightAutomatic各辺の重み
    Method Automatic使用するメソッド
  • Methodの使用可能な設定値には，"Dijkstra"，"FloydWarshall"，"Johnson"がある．

例題

すべて開く すべて閉じる

例  (1)

ペテルセン(Petersen)グラフの距離行列を与える：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

スコープ  (8)

GraphDistanceMatrixは無向グラフに使うことができる：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

有向グラフ：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

重み付きグラフ：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

多重グラフ：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

混合グラフ：

Wolfram Language code: GraphDistanceMatrix[[image]]//MatrixForm

規則を使ってグラフを指定する：

Wolfram Language code: GraphDistanceMatrix[{1 -> 2, 2 -> 3, 3 -> 1, 3 -> 4, 4 -> 5, 3 -> 5}]//MatrixForm

それほど大きくないグラフの行列の列を1列抽出する：

Wolfram Language code: g = GridGraph[{10, 10}];Timing[GraphDistanceMatrix[g][[All, 1]]//Dimensions]

GraphDistanceを使って同じ計算をするとより時間がかかる：

Wolfram Language code: Timing[Table[GraphDistance[g, 1, v], {v, VertexList[g]}]//Dimensions]

GraphDistanceMatrixは大きいグラフに使うことができる：

Wolfram Language code: g = GridGraph[{10, 10, 10, 10}];
Wolfram Language code: Timing[GraphDistanceMatrix[g][[All, 1]]//Dimensions]

必要なのが1列のみのでグラフが大きい場合には，GraphDistanceを使った方が速い：

Wolfram Language code: Timing[Table[GraphDistance[g, 1, v], {v, VertexList[g]}]//Dimensions]

オプション  (6)

Method  (6)

メソッドは入力によって自動的に選ばれる：

Wolfram Language code: {PetersenGraph[4, 1, VertexShapeFunction -> "Name"], PetersenGraph[4, 1, EdgeWeight -> {4, 0, 3, 1, 3, 2, 7, 8, 5, 2, 1, 6}, VertexShapeFunction -> "Name"]}
Wolfram Language code: Table[GraphDistanceMatrix[g]//MatrixForm, {g, %}]

"UnitWeight"メソッドはすべての辺に重み1を使う：

Wolfram Language code: GridGraph[{2, 3}, EdgeWeight -> {5, 2, 2, 5, 1, 2, 2}, VertexShapeFunction -> "Name"]
Wolfram Language code: GraphDistanceMatrix[%, Method -> "UnitWeight"]//MatrixForm

"Dijkstra"は辺の重みが正のグラフにのみ使うことができる：

Wolfram Language code: GridGraph[{2, 3}, EdgeWeight -> {5, 2, 2, 5, 1, 2, 2}, VertexShapeFunction -> "Name"]
Wolfram Language code: GraphDistanceMatrix[%, Method -> "Dijkstra"]//MatrixForm

"FloydWarshall"は負の辺の重みを含む有向グラフに使うことができる：

Wolfram Language code: WeightedAdjacencyGraph[(| | | | | | | | - | - | -- | - | - | - | | ∞ | 2 | 5 | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | 2 | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 5 | ∞ | | ∞ | ∞ | -2 | ∞ | ∞ | 2 | | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 2 | ∞ |), VertexShapeFunction -> "Name", AbsoluteOptions[GridGraph[{2, 3}], VertexCoordinates]]
Wolfram Language code: GraphDistanceMatrix[%, Method -> "FloydWarshall"]//MatrixForm

"Johnson"は負の辺の重みを含む有向グラフに使うことができる：

Wolfram Language code: WeightedAdjacencyGraph[(| | | | | | | | - | - | -- | - | - | - | | ∞ | 2 | 5 | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | 2 | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 5 | ∞ | | ∞ | ∞ | -2 | ∞ | ∞ | 2 | | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 2 | ∞ |), VertexShapeFunction -> "Name", AbsoluteOptions[GridGraph[{2, 3}], VertexCoordinates]]
Wolfram Language code: GraphDistanceMatrix[%, Method -> "Johnson"]//MatrixForm

"Johnson"は疎なグラフでは"FloydWarshall"メソッドより速いことがある：

Wolfram Language code: StarGraph[6, EdgeWeight -> RandomReal[{1, 5}, 5]]
Wolfram Language code: GraphDistanceMatrix[%, Method -> "Johnson"]//MatrixForm

アプリケーション  (2)

グラフ全体を考慮して頂点離心率を求める：

Wolfram Language code: {a = PetersenGraph[7, 2, VertexSize -> {1 -> Medium}], b = Graph[Range[4], {12, 34}, VertexSize -> {1 -> Medium}], c = Graph[Range[3], {12, 32, 31}, VertexSize -> {1 -> Small}, EdgeStyle -> Arrowheads[Small]]}
Wolfram Language code: Table[Max[GraphDistanceMatrix[g][[1]]], {g, {a, b, c}}]

強連結グラフの場合，結果はVertexEccentricityのものと一致する：

Wolfram Language code: Table[VertexEccentricity[g, 1], {g, {a, b, c}}]

連結グラフのすべての頂点の頂点離心率を求める：

Wolfram Language code: g = GridGraph[{2, 3, 4}]
Wolfram Language code: Max /@ GraphDistanceMatrix[g]

結果を検証する：

Wolfram Language code: % === Table[VertexEccentricity[g, v], {v, VertexList[g]}]

特性と関係  (5)

距離行列の行と列はVertexListで与えられた順に従う：

Wolfram Language code: g = [image];
Wolfram Language code: VertexList[g]
Wolfram Language code: TableForm[GraphDistanceMatrix[g], TableHeadings -> {c = Style[#, Red]& /@ %, c}]

距離行列の対角項は常に0である：

Wolfram Language code: PetersenGraph[5, 2]
Wolfram Language code: Diagonal[GraphDistanceMatrix[%]]

GraphDistanceを使って距離行列を求めることができる：

Wolfram Language code: g = GridGraph[{2, 3}]
Wolfram Language code: Table[GraphDistance[g, i, j], {i, VertexList[g]}, {j, VertexList[g]}] == GraphDistanceMatrix[g]

連結グラフでは，頂点のVertexEccentricityは距離行列を使って計算できる：

Wolfram Language code: g = GridGraph[{3, 4}]
Wolfram Language code: GraphDistanceMatrix[g][[VertexIndex[g, 1], All]]//Max
Wolfram Language code: VertexEccentricity[g, 1]

別々の連結要素に属する2つの頂点間の距離はInfinityである：

Wolfram Language code: g = [image];
Wolfram Language code: ConnectedGraphQ[g]
Wolfram Language code: GraphDistanceMatrix[g]//MatrixForm

考えられる問題  (2)

行列指標と頂点の間には想定される対応関係がないことがある：

Wolfram Language code: g = Graph[{23, 12}, EdgeWeight -> {1, 10}, VertexShapeFunction -> "Name"]
Wolfram Language code: (d = GraphDistanceMatrix[g])//MatrixForm

2から3までの距離は予想される行列の位置にはない：

Wolfram Language code: GraphDistance[g, 2, 3] == d[[2, 3]]

理由は頂点が予想される順序ではないからである：

Wolfram Language code: VertexList[g]

Graph等の関数を呼ぶときに頂点を明示的に並べることで問題を解決する：

Wolfram Language code: h = Graph[Range[3], {23, 12}, EdgeWeight -> {1, 10}, VertexShapeFunction -> "Name"]
Wolfram Language code: VertexList[h]
Wolfram Language code: GraphDistanceMatrix[h]//MatrixForm

これで距離が予想される位置に求まるようになった：

Wolfram Language code: GraphDistance[h, 2, 3] == %[[2, 3]]

"BellmanFord"は有効なMethodオプションではない：

Wolfram Language code: g = WeightedAdjacencyGraph[(| | | | | | | | - | - | -- | - | - | - | | ∞ | 2 | 5 | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | 2 | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 5 | ∞ | | ∞ | ∞ | -2 | ∞ | ∞ | 2 | | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | | ∞ | ∞ | ∞ | ∞ | 2 | ∞ |), VertexShapeFunction -> "Name", AbsoluteOptions[GridGraph[{2, 3}], VertexCoordinates]]
Wolfram Language code: GraphDistanceMatrix[g, Method -> "BellmanFord"]//MatrixForm

代りに"FloydWarshall"，"Johnson"あるいはデフォルトで選択されるMethodを使う：

Wolfram Language code: GraphDistanceMatrix[g, Method -> "FloydWarshall"]//MatrixForm
Wolfram Language code: GraphDistanceMatrix[g, Method -> "Johnson"]//MatrixForm
Wolfram Language code: GraphDistanceMatrix[g]//MatrixForm

おもしろい例題  (1)

格子グラフのグラフ距離行列をプロットする：

Wolfram Language code: MatrixPlot[GraphDistanceMatrix[GridGraph[{20, 20}]]]

ナイトグラフをプロットする：

Wolfram Language code: MatrixPlot[GraphDistanceMatrix[KnightTourGraph[20, 20]]]
Wolfram Research (2010), GraphDistanceMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html （2015年に更新）.

テキスト

Wolfram Research (2010), GraphDistanceMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html （2015年に更新）.

CMS

Wolfram Language. 2010. "GraphDistanceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html.

APA

Wolfram Language. (2010). GraphDistanceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html

BibTeX

@misc{reference.wolfram_2026_graphdistancematrix, author="Wolfram Research", title="{GraphDistanceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}", note=[Accessed: 04-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_graphdistancematrix, organization={Wolfram Research}, title={GraphDistanceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDistanceMatrix.html}, note=[Accessed: 04-November-2026]}