HeavisidePi
HeavisidePi[x]
![]() で1に等しく
で1に等しく![]() では0に等しいボックス分布
では0に等しいボックス分布![]() を表す.
を表す.
HeavisidePi[x1,x2,…]
すべてが![]() であれば1に等しい多次元ボックス分布
であれば1に等しい多次元ボックス分布![]() を表す.
を表す.
詳細
- HeavisidePi[x]は,-1/2と1/2以外のすべての数 x に対して0または1を返す.
- HeavisidePi[x]はHeavisideTheta[
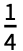 -x2]に等しい.
-x2]に等しい. - HeavisidePiは,微分係数,積分,積分変換,微分方程式に使うことができる.
- HeavisidePiは属性Orderlessを持つ.
例題
すべて開くすべて閉じる例 (4)
スコープ (38)
数値評価 (6)
HeavisidePiは常に厳密な結果を返す:
HeavisidePiはリストに縫い込まれる:
Aroundを使って平均的な場合の統計区間を計算する:
MatrixFunctionを使って行列のHeavisidePi関数を計算することもできる:
特定の値 (4)
可視化 (4)
HeavisidePi関数をプロットする:
スケールされたHeavisidePi関数を可視化する:
HeavisidePiと周期関数の組合せを可視化する:
HeavisidePiを三次元でプロットする:
関数の特性 (12)
HeavisidePi関数の定義域:
HeavisidePi関数の値域:
HeavisidePiは偶関数である:
HeavisidePiの下の面積は1である:
HeavisidePiは点 ![]() でジャンプの不連続性を持つ:
でジャンプの不連続性を持つ:
HeavisidePiは解析関数ではない:
HeavisidePiは非増加でも非減少でもない:
HeavisidePiは単射ではない:
HeavisidePiは全射ではない:
HeavisidePiは非負でも非正でもない:
HeavisidePiは凸でも凹でもない:
TraditionalFormによる表示:
微分 (4)
積分 (4)
積分変換 (4)
単位ボックスのFourierTransformはSinc関数である:
単位ボックスのLaplaceTransformを求める:
HeavisidePiのそれ自身によるたたみ込みはHeavisideLambdaである:
アプリケーション (2)
特性と関係 (2)
テキスト
Wolfram Research (2008), HeavisidePi, Wolfram言語関数, https://reference.wolfram.com/language/ref/HeavisidePi.html.
CMS
Wolfram Language. 2008. "HeavisidePi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeavisidePi.html.
APA
Wolfram Language. (2008). HeavisidePi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeavisidePi.html