HistogramDistribution

HistogramDistribution[{x1,x2,…}]

データ値 xiのヒストグラムに対応する確率分布を表す．

HistogramDistribution[{{x1,y1,…},{x2,y2,…},…}]

データ値{xi,yi,…}に基づく多変量ヒストグラム分布を表す．

HistogramDistribution[…,bspec]

bspec で指定されるビンのヒストグラム分布を表す．

詳細

  • HistogramDistributionは他の確率分布と同じように使えるDataDistributionオブジェクトを返す．
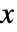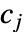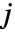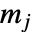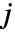  • HistogramDistributionの値 についての確率密度関数はsum_(j=1)^m(c_j)/(n m_j) Boole[b_(j-1)<=x<b_j]で与えられる．ただし，はビン 中のデータ点の数，はビン の幅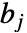，はビンデリミタ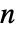， はデータ点の総数である．
  • 各ビンの 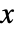幅は xiの値に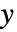， の幅は yiに等，それぞれに基づいて計算される．
  • 使用可能なビン指定 bspec
  • nn 個のビンを使う
    {w}幅が w のビンを使う
    {min,max,w}min から max まで幅 w のビンを使う
    {{b1,b2,…}}ビン[b1,b2),[b2,b3),…を使う
    Automaticビン幅を自動的に決定する
    "name"名前付きのビン分割メソッドを使う
    fw明示的なビン指定{b1,b2,…}を得るために fw を適用する
    {xspec,yspec,…}x, y 等の異なる指定を使う
  • 使用可能な名前付きビンメソッド
  • "FreedmanDiaconis"四分位範囲をサンプルサイズの立方根で割ったものの2倍
    "Knuth"区分的一様モデルの尤度と事前確率のバランスを取る
    "Scott"平均二乗誤差を漸近的に最小化する
    "Sturges"データの長さに基づいたビンの数を計算する
    "Wand"1レベルで再帰的に近似したWandの方法
  • ヒストグラム分布における値 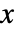の確率密度は区分的定数関数である．
  • HistogramDistributionはMean，CDF，RandomVariate等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (2)

一変量データのヒストグラム分布を作成する：

結果の分布を使って分布関数の可視化を含む解析を行う：

モーメントと分位数を計算する：

二変量データのヒストグラム分布を作成する：

確率密度関数と累積分布関数を可視化する：

共分散と一般化されたモーメントを計算する：

スコープ  (29)

基本的な用法  (5)

あるデータのヒストグラムから分布を作成する：

分布から確率を計算する：

単位付きの数量データからヒストグラム分布を作る：

記述統計量を求め，選ぶ：

ビンの数を減らして局所感度を低下させる：

ビン幅を広くして局所感度を低下させる：

より高次元のヒストグラムから分布を作成する：

一変量周辺分布の確率密度関数をプロットする：

二変量周辺分布の確率密度関数をプロットする：

分布特性  (10)

分布関数を推定する：

分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

分位関数：

特殊な分位値：

乱数を生成する：

HistogramDistributionと比較する：

確率と推定値を計算する：

母関数：

二変量データの分布関数を推定する：

二変量分布のモーメントを計算する：

特殊なモーメント：

一般的なモーメント：

乱数を生成する：

点分布を示す：

ビンの数が少ない程もとになっている分布の粗い近似となる：

母関数：

ビン分割  (14)

ビンの数を自動的に計算する：

データが多いとビンが小さくなる：

使用するビンの数を明示的に指定する：

それぞれ5と50のビンを指定する：

ビンの幅を明示的に指定する：

ビン幅1.と0.1を使う：

ビンの範囲と幅を指定する：

固定区間でそれぞれ1.5と.15のビン幅を使う：

明示的なビンデリミタを与える：

別々の自動的なビン分割メソッドを使う：

ビン関数を使って整数の境界でビンを区切る：

二変量データのビンの数を自動的に計算する：

データが多いとビンが小さくなる：

使用するビンの数を明示的に指定する：

ビンの幅を明示的に指定する：

ビン範囲とビン幅を指定する：

ビンデリミタを明示的に与える：

異なる自動ビン分割メソッドを使う：

各次元で異なるビン指定を使う：

行次元で3ビン，列次元でビン幅0.5を使う：

アプリケーション  (6)

推定密度と理論モデルを比較する：

ヒト染色体の長さの分布：

配列の長さが15よりも大きくなる確率を計算する：

いくつかの品詞について単語長の分布を比較する：

無作為に選ばれた英語の名詞の期待される文字数：

S&P 500指標の日ごとのポイント変化の分布を推定する：

指定された日に1%ポイント以上変化する確率を計算する：

KnuthのBayesianメソッドで二峰性データに使うビンの数を決定する：

最適数のビンは後部密度の対数を最大化する：

Knuthメソッド，Scottの規則，Freedman–Diaconis規則を使った密度推定：

LogLikelihoodに関してはKnuthメソッドが他の2つに比べてはるかに優っている：

経験累積分布関数の連続版を構築する：

HistogramDistributionについての累積分布関数は区分的に線形である：

2つの分布間のCramer–von Mises距離を計算する：

特性と関係  (10)

HistogramDistributionの確率密度関数は確率密度Histogramに等しい：

結果の密度推定を積分すると1になる：

出力精度はデータ精度に一致する：

確率密度関数は区分定数である：

累積分布関数とSurvivalFunctionは区分線形である：

HazardFunctionは線形分数関数である：

HistogramDistributionは一様分布数のMixtureDistributionである：

HistogramDistributionはもとの分布の一定した推定器である：

HistogramDistributionは，入力がTimeSeriesのときにのみ値に使うことができる：

値のヒストグラム分布を比較する：

HistogramDistributionは，入力がTemporalDataのときは，すべての値に同時に働く：

計算されたヒストグラム分布をすべての経路からの値と比較する：

考えられる問題  (1)

ビン範囲を指定することでデータを推定から落とすことができる：

幅だけを指定してもデータはすべて使われる：

おもしろい例題  (1)

HistogramDistributionを使ったランダムなポップアート：

Wolfram Research (2010), HistogramDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/HistogramDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), HistogramDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/HistogramDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "HistogramDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HistogramDistribution.html.

APA

Wolfram Language. (2010). HistogramDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HistogramDistribution.html

BibTeX

@misc{reference.wolfram_2024_histogramdistribution, author="Wolfram Research", title="{HistogramDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HistogramDistribution.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_histogramdistribution, organization={Wolfram Research}, title={HistogramDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HistogramDistribution.html}, note=[Accessed: 04-November-2024 ]}