HistogramDistribution

HistogramDistribution[{x1,x2,…}]

表示与数据值 xi 的直方图对应的概率分布.

HistogramDistribution[{{x1,y1,…},{x2,y2,…},…}]

表示基于数据值 {xi,yi,…} 的多变量直方图分布.

HistogramDistribution[…,bspec]

表示分组方法由 bspec 指定的直方图分布.

更多信息

  • HistogramDistribution 返回 DataDistribution 对象，用法和任意其它概率分布一样.
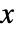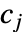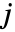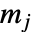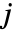  • 值 的 HistogramDistribution 的概率密度函数由 sum_(j=1)^m(c_j)/(n m_j) Boole[b_(j-1)<=x<b_j] 给出，其中 为直方条 中的数据点个数， 为直方条 的宽度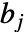， 为分组界限值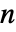， 为数据点的总数.
  • 各箱 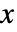方向的宽根据值 xi 计算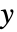， 方向的宽度根据值 yi 计算，依此类推.
  • 可以给出下列分组规范 bspec：
  • n分成 n 组
    {w}组距为 w
    {min,max,w}在 min 到 max 的范围内使用宽度为 w 的直方条
    {{b1,b2,…}}使用界限值 [b1,b2),[b2,b3),… 分组
    Automatic自动确定组距
    "name"使用已命名的分组方法
    fw应用 fw 以得到明确的分组规定 {b1,b2,…}
    {xspec,yspec,…}给出不同的 x、y 等的规范
  • 可能的已命名的分组方法包括：
  • "FreedmanDiaconis"四分间距的两倍除以样本大小的立方根
    "Knuth"平衡分段均匀模型的似然值和先验概率
    "Scott"渐近最小化均方误差
    "Sturges"根据数据长度计算组数
    "Wand"一级递归近似 Wand 分组方法
  • 在直方图分布中，值 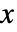的概率密度为分段常数函数.
  • HistogramDistribution 可以与 Mean、CDF 和 RandomVariate 等函数配合使用.

范例

打开所有单元关闭所有单元

基本范例  (2)

创建单变量数据的直方图分布：

对得到的分布进行分析，包括可视化分布函数：

计算矩和分位数：

创建双变量数据的直方图分布：

可视化 PDF 和 CDF：

计算协方差和一般矩：

范围  (29)

基本用途  (5)

从一些数据组成的直方图中创建一个分布：

根据该分布计算概率：

根据数量数据创建直方图分布：

给出描述统计量：

减少组数以降低局部敏感度：

增大组距以降低局部敏感度：

在较高维度下根据直方图创建分布：

绘制单变量边缘分布的概率密度函数：

绘制双变量边缘分布的概率密度函数：

分布属性  (10)

估计分布函数：

计算分布的矩：

特殊矩：

一般矩：

分位数函数：

特殊分位数值：

生成随机数：

与 HistogramDistribution 比较：

计算概率和期望：

母函数：

估计双变量数据的分布函数：

计算双变量分布的矩：

特殊矩：

一般矩：

生成随机数：

显示点分布：

组数越少，对底层分布的近似越粗略：

母函数：

分组  (14)

自动计算组数：

数据越多，组距越小：

明确指定组数：

分别指定5个和50个组：

明确指定组距：

组距为1.和0.1：

指定范围和组距：

在固定区间上，分别使用1.5和.15作为组距：

明确指定分组界限：

使用不同的自动分组方法：

使用分组函数使分组界限落在整数上：

自动计算双变量数据的组数：

数据越多，组距越小：

明确指定组数：

明确指定组距：

指定分组范围和组距：

明确指定分组界限：

使用不同的自动分组方法：

在各维使用不同的分组规范：

在行向维度上指定3个组，在列向维度上指定组距为0.5：

应用  (6)

把估计的密度与理论模型作比较：

人类染色体的长度分布：

计算序列长度大于15的概率：

比较演讲中各种词性单词的长度分布：

一个随机选择的英文名词的字母个数期望值：

估计标普 500 指数每日点数变化的分布：

计算给定的一天内点数变化为 1% 或者更多的概率：

利用 Knuth 贝叶斯方法确定用于双峰数据的组数：

最佳组数使后验密度的对数最大化：

利用 Knuth 方法、Scott 规则和 Freedman-Diaconis 规则的密度估计：

Knuth 方法在 LogLikelihood 上的性能超过其它两个：

构建一个连续的经验累积分布函数：

HistogramDistribution 的累积分布函数是分段线性的：

计算两个分布之间的 Cramer–von Mises 距离：

属性和关系  (10)

HistogramDistribution 的 PDF 等价于概率密度的 Histogram：

得到的密度估计积分为 1：

输出精度与数据精度一致：

PDF 是分段常数函数：

CDF 与 SurvivalFunction 是分段线性函数：

HazardFunction 是线性分式函数：

HistogramDistribution 是均匀分布的 MixtureDistribution：

HistogramDistribution 是底层分布的相容估计量：

当输入是 TimeSeries 时 HistogramDistribution 只能用于数值：

与值的直方图分布比较：

当输入是 TemporalData 时 HistogramDistribution 适用于所有的值：

和根据所有路径上的值计算得到的直方图分布比较：

可能存在的问题  (1)

有可能因为指定分组范围从估计中丢掉数据：

仅指定组距则得以运用所有的数据：

巧妙范例  (1)

采用 HistogramDistribution 的随机波普艺术：

Wolfram Research (2010)，HistogramDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HistogramDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，HistogramDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HistogramDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "HistogramDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/HistogramDistribution.html.

APA

Wolfram 语言. (2010). HistogramDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HistogramDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_histogramdistribution, author="Wolfram Research", title="{HistogramDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HistogramDistribution.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_histogramdistribution, organization={Wolfram Research}, title={HistogramDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HistogramDistribution.html}, note=[Accessed: 04-November-2024 ]}