InterpolatingPolynomial
InterpolatingPolynomial[{f1,f2,…},x]
constructs an interpolating polynomial in x which reproduces the function values ![]() at successive integer values 1, 2, … of
at successive integer values 1, 2, … of ![]() .
.
InterpolatingPolynomial[{{x1,f1},{x2,f2},…},x]
constructs an interpolating polynomial for the function values ![]() corresponding to
corresponding to ![]() values
values ![]() .
.
InterpolatingPolynomial[{{{x1,y1,…},f1},{{x2,y2,…},f2},…},{x,y,…}]
constructs a multidimensional interpolating polynomial in the variables x, y, ….
InterpolatingPolynomial[{{{x1,…},f1,df1,…},…},{x,…}]
constructs an interpolating polynomial that reproduces derivatives as well as function values.
Details and Options

- The function values
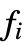 and sample points
and sample points 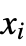 , etc. can be arbitrary real or complex numbers, and in 1D can be arbitrary symbolic expressions.
, etc. can be arbitrary real or complex numbers, and in 1D can be arbitrary symbolic expressions. - With a 1D list of data of length
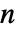 , InterpolatingPolynomial gives a polynomial of degree
, InterpolatingPolynomial gives a polynomial of degree 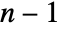 .
. - With any given specified set of data, there are infinitely many possible interpolating polynomials; InterpolatingPolynomial always tries to find the one with lowest total degree.
- InterpolatingPolynomial gives the interpolating polynomial in a Horner form, suitable for numerical evaluation.
- Different elements in the data can have different numbers of derivatives specified.
- For multidimensional data, the
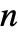
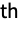 derivative can be given as a tensor with a structure corresponding to D[f,{{x,y,…},n}]. »
derivative can be given as a tensor with a structure corresponding to D[f,{{x,y,…},n}]. » - InterpolatingPolynomial allows any function value or derivative to be given as Automatic, in which case it will attempt to fill in the necessary information from derivatives or other function values. »
- The option setting Modulus->n specifies that the interpolating polynomial should be found modulo
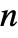 . »
. »
Examples
open allclose allBasic Examples (2)
Scope (3)
Generalizations & Extensions (3)
Options (1)
Applications (5)
Construct a polynomial with roots a, b, and c:
Newton–Cotes integration formulas with ![]() points:
points:
Centered finite difference formula of order ![]() for approximating the first derivative:
for approximating the first derivative:
Interpolate to find the characteristic polynomial of a matrix:
Create a tensor product interpolation:
Create an interpolating polynomial for each fixed ![]() value:
value:
Show the interpolation curves in the ![]() direction:
direction:
Properties & Relations (3)
The interpolating polynomial always goes through the data points:
ListInterpolation creates a tensor product interpolation:
Create a numerical InterpolatingFunction object:
Create a symbolic polynomial by interpolating in each dimension separately:
Verify that results agree with random data points:
Choose some points to be interpolated:
Use VandermondeMatrix in LinearSolve to obtain the coefficients of the interpolating polynomial:
Possible Issues (3)
Sampling at evenly spaced intervals in the interval from ![]() to
to ![]() :
:
The polynomial that interpolates these points has large oscillations:
Interpolation uses a lower-order piecewise polynomial that does not have this problem:
When derivatives are specified without function values an interpolant may not be found:
There is no quadratic polynomial that satisfies the interpolation conditions:
Points with abscissas lying on a line in 2 dimensions:
In multiple dimensions an interpolant may not be found for some arrangements of points:
This polynomial interpolates the data above, but has total degree 2:
Text
Wolfram Research (1991), InterpolatingPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html (updated 2007).
CMS
Wolfram Language. 1991. "InterpolatingPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html.
APA
Wolfram Language. (1991). InterpolatingPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html