WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

InterpolatingPolynomial[{f1,f2,…},x]

x の連続する整数値1, 2, … について関数の値 fiを再生する x における補間多項式を構築する．

InterpolatingPolynomial[{{x1,f1},{x2,f2},…},x]

x の値 xiに対応する関数の値 fiについての補間多項式を構築する．

InterpolatingPolynomial[{{{x1,y1,…},f1},{{x2,y2,…},f2},…},{x,y,…}]

変数 x, y, …における多次元補間多項式を構築する．

InterpolatingPolynomial[{{{x1,…},f1,df1,…},…},{x,…}]

関数の値とともに導関数も再生する補間多項式を構築する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
一般化と拡張  
オプション  
Modulus  
アプリケーション  
特性と関係  
考えられる問題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

InterpolatingPolynomial

InterpolatingPolynomial[{f1,f2,…},x]

x の連続する整数値1, 2, … について関数の値 fiを再生する x における補間多項式を構築する．

InterpolatingPolynomial[{{x1,f1},{x2,f2},…},x]

x の値 xiに対応する関数の値 fiについての補間多項式を構築する．

InterpolatingPolynomial[{{{x1,y1,…},f1},{{x2,y2,…},f2},…},{x,y,…}]

変数 x, y, …における多次元補間多項式を構築する．

InterpolatingPolynomial[{{{x1,…},f1,df1,…},…},{x,…}]

関数の値とともに導関数も再生する補間多項式を構築する．

詳細とオプション

  • 関数の値 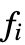f_(i)とサンプル点 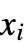x_(i)等は，任意の実数あるいは複素数でよく，一次元では任意の記号式でもよい．
  • 長さ 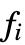の一次元のデータリストで，InterpolatingPolynomialは次数 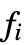の多項式を与える．
  • 指定された任意のデータセットを使ってできる補間多項式は無限にある．InterpolatingPolynomialは，常にその中で総次数が最も低いものを見付けようとする．
  • InterpolatingPolynomialは，数値的評価に適したホーナー形式の補間多項式を与える．
  • データ中の異なる要素は指定された異なる数の導関数を持つことができる．
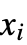
  • 多次元データに関しては，D[f,{{x,y,…},n}]に相当する構造を持ったテンソルとして 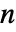n 次導関数を与えることができる． »
  • InterpolatingPolynomialは任意の関数値あるいは導関数がAutomaticとして与えられるのを許す．この場合，必要な情報は導関数あるいは他の関数値から得ようとされる． »
  • Modulus->n というオプション設定は，補間多項式の法が 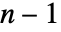n であるように指定する． »

例題

すべて開く すべて閉じる

例  (2)

正方形の補間多項式を構築する：

Wolfram Language code: InterpolatingPolynomial[{1, 4, 9, 16}, x]

結果を検証する：

Wolfram Language code: Expand[%]

3点から補間多項式を構築する：

Wolfram Language code: InterpolatingPolynomial[{{-1, 4}, {0, 2}, {1, 6}}, x]

1点で結果を検証する：

Wolfram Language code: % /. x -> 0

スコープ  (3)

Wolfram Language code: InterpolatingPolynomial[{4, 7, 2, 8, 9}, x]
Wolfram Language code: Show[Plot[%, {x, 0, 6}], ListPlot[{4, 7, 2, 8, 9}]]

多項式の値が8のときに導関数0を持つようにする：

Wolfram Language code: InterpolatingPolynomial[{4, 7, 2, {8, 0}, 9}, x]
Wolfram Language code: Show[Plot[%, {x, 0, 6}], ListPlot[{4, 7, 2, 8, 9}]]

2つの変数に依存して補間された値：

Wolfram Language code: InterpolatingPolynomial[{{{0, 0}, 1}, {{1, 0}, 7}, {{0, 1}, 10}, {{2, 1}, 40}, {{3, 3}, 151}, {{1, 2}, 47}}, {x, y}]
Wolfram Language code: ContourPlot[%, {x, 0, 3}, {y, 0, 3}, Epilog -> {Green, Map[Point, {{0, 0}, {1, 0}, {0, 1}, {2, 1}, {3, 3}, {1, 2}}]}]

一般化と拡張  (3)

多項式がとで導関数を持たないようにする，ただしそこでの値は指定しない：

Wolfram Language code: InterpolatingPolynomial[{{-1, Automatic, 0}, {0, 1, 1}, {1, Automatic, 0}}, x]
Wolfram Language code: Plot[%, {x, -1, 1}]

二次元での偏導関数のいくつかを指定する：

Wolfram Language code: InterpolatingPolynomial[{{{0, 0}, 1, {2, 3}}, {{1, 0}, 7}, {{0, 1}, 10, {Automatic, 15}}}, {x, y}]

3つの変数で値と傾斜を補間する：

Wolfram Language code: InterpolatingPolynomial[{{{1, 2, 3}, 4, {5, 6, 7}}, {{3, 2, 1}, 0}}, {x, y, z}]

オプション  (1)

Modulus  (1)

47を法とする算術で与えられた点を補間する多項式を求める：

Wolfram Language code: p = InterpolatingPolynomial[{{0, 1}, {4, 2}, {9, 3}, {16, 4}}, x, Modulus -> 47]

この多項式は指定された47を法とする値を取る：

Wolfram Language code: p /. x -> {0, 4, 9, 16}
Wolfram Language code: Mod[%, 47]

アプリケーション  (5)

根a，b，cを持つ多項式を構築する：

Wolfram Language code: InterpolatingPolynomial[{{0, 1}, {a, 0}, {b, 0}, {c, 0}}, x]
Wolfram Language code: Factor[%]

点のニュートン・コーツ(Newton-Cotes)積分公式：

Wolfram Language code: TableForm[Table[ abc = Range[0, n - 1] / (n - 1); Integrate[InterpolatingPolynomial[Table[{x, f[x]}, {x, abc}], x], {x, 0, 1}], {n, 2, 8}]]

第1導関数を近似するための 階の中心有限差分公式：

Wolfram Language code: TableForm[Table[ abc = Range[-k / 2, k / 2]; Together[D[InterpolatingPolynomial[Table[{s, f[x + s h]}, {s, abc}], s], s] / h /. s -> 0], {k, 2, 10, 2}]]

行列の固有多項式を求めるために補間する：

Wolfram Language code: m = RandomInteger[1, {6, 6}]
Wolfram Language code: InterpolatingPolynomial[Table[Det[m - λ IdentityMatrix[6]], {λ, 11}], x]
Wolfram Language code: Expand[%] === CharacteristicPolynomial[m, x]

テンソル積の補間を作成する：

Wolfram Language code: {m, n} = {4, 4}; {xc, yc} = {Range[m], Range[n]}; zc = RandomInteger[{-9, 9}, {m, n}];

固定されたの 値それぞれについて補間多項式を作成する：

Wolfram Language code: yinterp = Map[InterpolatingPolynomial[Transpose[{yc, #}], y]&, zc]

方向の補間曲線を示す：

Wolfram Language code: points = Graphics3D[{PointSize[Medium], Red, Point@Flatten[Table[{xc[[i]], yc[[j]], zc[[i, j]]}, {i, m}, {j, n}], 1]}];
Wolfram Language code: Show[ParametricPlot3D[Evaluate@Table[{xc[[i]], y, yinterp[[i]]}, {i, m}], {y, 1, n}, BoxRatios -> {1, 1, 0.4}], points]

方向の曲線間を補間する：

Wolfram Language code: xyinterp = InterpolatingPolynomial[Transpose[{xc, yinterp}], x]

補間曲面とデータ点を示す：

Wolfram Language code: Show[Plot3D[xyinterp, {x, 1, m}, {y, 1, n}], points]

特性と関係  (3)

補間多項式は常にデータ点を通る：

Wolfram Language code: data = {1, 2, 3, 5, 8, 5};
Wolfram Language code: InterpolatingPolynomial[data, x]
Wolfram Language code: % /. x -> Range[6]

ListInterpolationはテンソル積の補間を作る：

Wolfram Language code: {m, n} = {5, 6}; {xc, yc} = {Range[m], Range[n]}; zc = RandomInteger[{-9, 9}, {m, n}];

数値InterpolatingFunctionオブジェクトを作る：

Wolfram Language code: linterp = ListInterpolation[zc, {xc, yc}, InterpolationOrder -> {m - 1, n - 1}]

各次元で別々に補間することで記号多項式を作る：

Wolfram Language code: yinterp = Map[InterpolatingPolynomial[Transpose[{yc, #}], y]&, zc]; interp = InterpolatingPolynomial[Transpose[{xc, yinterp}], x];

結果がランダムなデータ点に一致することを証明する：

Wolfram Language code: Max[Abs[Table[interp - linterp[x, y], {x, RandomReal[{1, m}, 2m]}, {y, RandomReal[{1, n}, 2n]}]]]

補間する点を数点選ぶ：

Wolfram Language code: pts = {{0, 0}, {1 / 10, 3 / 10}, {1 / 2, 3 / 5}, {1, -1 / 5}, {2, 3}};

LinearSolveでVandermondeMatrixを使って補間多項式の係数を取得する：

Wolfram Language code: LinearSolve[VandermondeMatrix[pts[[All, 1]]], pts[[All, 2]]]
Wolfram Language code: % == CoefficientList[InterpolatingPolynomial[pts, x], x]

考えられる問題  (3)

ルンゲ(Runge)関数：

Wolfram Language code: f[x_] := 1 / (1 + 25 x ^ 2);

からまでの区間で等間隔にサンプルを取る：

Wolfram Language code: points = Table[{x, f[x]}, {x, -1, 1, .1}];

これらの点を補間する多項式には大きい振動がある：

Wolfram Language code: Plot[Evaluate[InterpolatingPolynomial[points, x]], {x, -1, 1}, PlotRange -> All, Epilog -> {Red, Map[Point, points]}]

Interpolationは，この問題のない，より階数の低い区分多項式を使う：

Wolfram Language code: Interpolation[points]
Wolfram Language code: Plot[%[x], {x, -1, 1}, Epilog -> {Red, Map[Point, points]}]

導関数が関数の値なしで指定されると，補間式が見付からないことがある：

Wolfram Language code: InterpolatingPolynomial[{{-1, 1}, {0, Automatic, 0}, {1, -1}}, x]

補間条件を満足する二次多項式は存在しない：

Wolfram Language code: Expand[InterpolatingPolynomial[{{-1, 1}, {0, a, 0}, {1, -1}}, x]]

二次元の線上にある横座標の点：

Wolfram Language code: data = {{{0, 0}, 1}, {{1, 1}, 2}, {{2, 2}, 4}};

多次元では，ある種の点の並び方では補間式が求まらないことがある：

Wolfram Language code: InterpolatingPolynomial[data, {x, y}]

この多項式は上記のデータを補間するが，全次数は2である：

Wolfram Language code: InterpolatingPolynomial[{{0, 1}, {1, 2}, {2, 4}}, x]
Wolfram Research (1991), InterpolatingPolynomial, Wolfram言語関数， https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html （2007年に更新）.

テキスト

Wolfram Research (1991), InterpolatingPolynomial, Wolfram言語関数， https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html （2007年に更新）.

CMS

Wolfram Language. 1991. "InterpolatingPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html.

APA

Wolfram Language. (1991). InterpolatingPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html

BibTeX

@misc{reference.wolfram_2026_interpolatingpolynomial, author="Wolfram Research", title="{InterpolatingPolynomial}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html}", note=[Accessed: 05-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_interpolatingpolynomial, organization={Wolfram Research}, title={InterpolatingPolynomial}, year={2007}, url={https://reference.wolfram.com/language/ref/InterpolatingPolynomial.html}, note=[Accessed: 05-November-2026]}