LQGRegulator
LQGRegulator[sspec,cvs,wts]
使用噪声协方差矩阵 cvs 为随机系统规范 sspec 给出最优输出反馈控制器,该矩阵使用权重 wts 最小化代价函数.
LQGRegulator[…,"prop"]
给出属性 "prop" 的值.
更多信息和选项




- LQGRegulator 也被称为线性二次型高斯控制器或随机线性控制器.
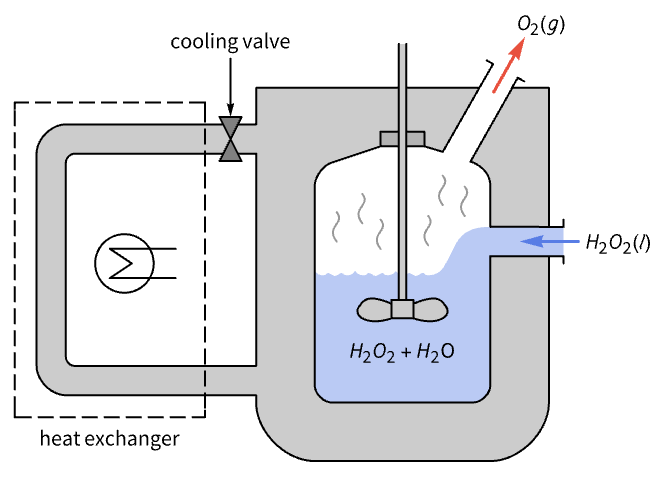
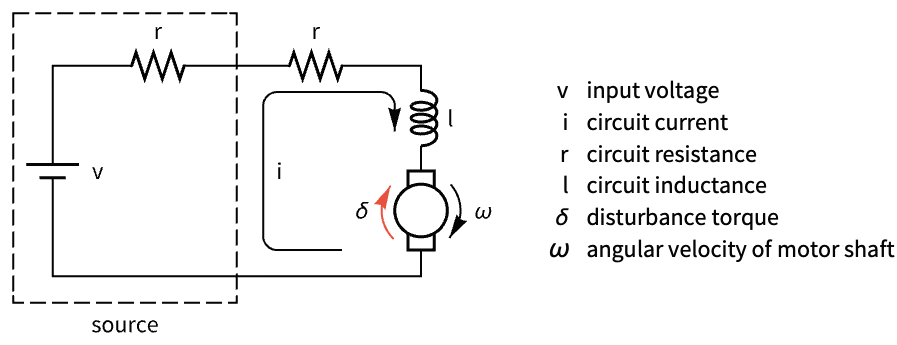
- LQGRegulator 用于计算具有扰动和测量噪声的系统的调节控制器或跟踪控制器,建模为零均值、高斯、白噪声过程.
- LQGRegulator 通过最小化状态和反馈输入的二次成本函数以及实际状态和估计状态之间的误差方差之和起作用.
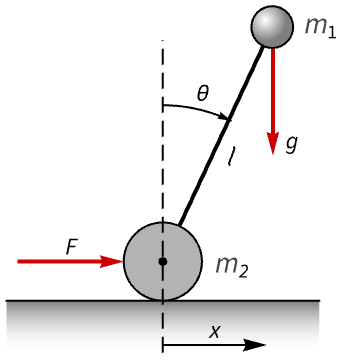
- 调节控制器旨在有扰动 uw 和 ue 进行干扰的情况下保持系统处于平衡状态. 典型范例包括将倒立摆保持在直立位置或保持飞机水平飞行.
- 调节控制器由形式为
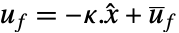 的控制律给出,其中
的控制律给出,其中 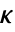 是计算得到的增益矩阵.
是计算得到的增益矩阵. - 状态 x 和反馈输入 uf 的权重为 q、r 和 p 的二次成本函数:
-
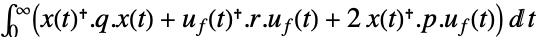
连续时间系统 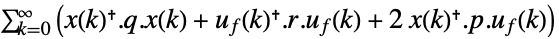
离散时间系统 - 跟踪控制器旨在有 uw 和 ue 干扰的情况下跟踪参考信号. 典型范例包括汽车的巡航控制系统或机器人的路径跟踪.
- 跟踪控制器由形式为
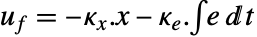 的控制律给出,其中
的控制律给出,其中 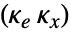 是为增强系统计算的增益矩阵,包括系统 sys 以及
是为增强系统计算的增益矩阵,包括系统 sys 以及 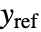 .
. - 增强状态
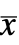 和反馈输入 uf 的权重为 q、r 和 p 的二次成本函数:
和反馈输入 uf 的权重为 q、r 和 p 的二次成本函数: -
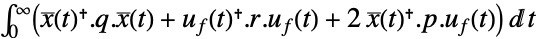
连续时间系统 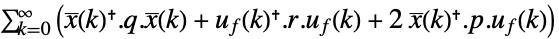
离散时间系统 - 增广系统的状态数由
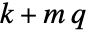 给出,其中
给出,其中 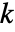 由 sys 的 SystemsModelOrder 给出,
由 sys 的 SystemsModelOrder 给出,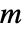 由 yref 的阶数给出,
由 yref 的阶数给出, 由信号 yref 的数量给出.
由信号 yref 的数量给出. - 权重矩阵的选择会导致性能和控制效果之间的折衷,并通过迭代获得好的设计. 其起始值可以是带有项
![TemplateBox[{{1, /, z}, i, 2}, Subsuperscript] TemplateBox[{{1, /, z}, i, 2}, Subsuperscript]](Files/LQGRegulator.zh/19.png) 的对角矩阵,其中 zi 是对应的 xi 或 ui 的最大允许绝对值.
的对角矩阵,其中 zi 是对应的 xi 或 ui 的最大允许绝对值. - 权重 wts 可以有如下形式:
-
{q,r} 没有交叉耦合的代价函数 {q,r,p} 有交叉耦合矩阵 p 的代价函数 - 测量 ym 可建模为
 ,其中
,其中 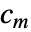 和
和 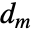 是与
是与 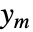 关联的
关联的 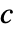 和
和  的子矩阵,
的子矩阵, 是噪声.
是噪声. - 随机输入 uw 和测量噪声 yv 看做是是零均值、白色和高斯噪声:
-
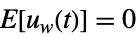 ,
, 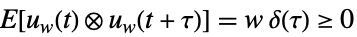
过程噪声 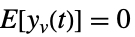 ,
, 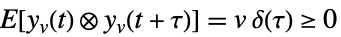
测量噪声 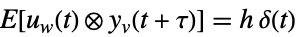
互协方差 - 协方差矩阵 cvs 可以有下列形式:
-
{w,v} 协方差矩阵和零互协方差 {w,v,h} 协方差和互协方差矩阵 - 系统规范 sspec 是系统 sys 以及 uf、ue、yt 和 yref 规范.
- 系统规范 sspec 可有如下形式:
-
StateSpaceModel[…] 线性控制输入和线性状态 AffineStateSpaceModel[…] 线性控制输入和非线性状态 NonlinearStateSpaceModel[…] 非线性控制输入和非线性状态 SystemModel[…] 通用系统模型 <…> 以 Association 形式给出的详细系统规范 - 详细系统规范可以有如下密钥:
-
"InputModel" sys 模型中的任意一个 "FeedbackInputs" All 反馈输入 uf "ExogenousInputs" None 外源输入 ue "MeasuredOutputs" All 测量输出 ym "TrackedOutputs" None 跟踪输出 yt "TrackedSignal" Automatic yref 的动态 - 输入和输出可有如下形式:
-
{num1,…,numn} StateSpaceModel,AffineStateSpaceModel 和 NonlinearStateSpaceModel 使用的有编号的输入或输出 numi {name1,…,namen} SystemModel 使用的有名输入或输出 namei All 使用所有输入或输出 None 不使用输入和输出 - LQGRegulator[…,"Data"] 返回可使用形式 cd["prop"] 用来提取额外属性的 SystemsModelControllerData 对象 cd.
- LQGRegulator[…,"prop"] 可直接用于获取 cd["prop"] 的值.
- 属性 "prop" 的可能值包括:
-
"ClosedLoopPoles" "ClosedLoopSystem" 的极点 "ClosedLoopSystem" 系统 csys {"ClosedLoopSystem",cspec} 对闭环系统形式的具体控制 "ControllerModel" 模型 cm "Design" 控制器设计的类型 "EstimatorGains" 增益矩阵 ℓ "EstimatorGainsDesignModel" 用于估值器增益设计的模型 "EstimatorRegulatorFeedbackModel" ue、ym 作为输入 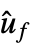 作为输出的模型
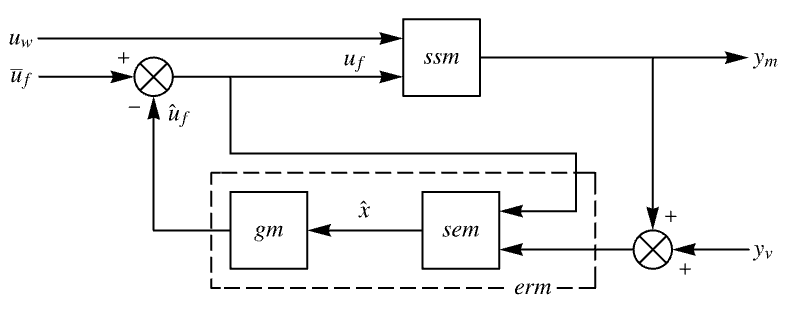
作为输出的模型"EstimatorRegulatorModel" uf、ue、ym 作为输入且 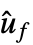 作为输出的模型 erm
作为输出的模型 erm"ExogenousInputs" sys 的确定和非反馈输入 ue "FeedbackGains" 增益矩阵 κ 或其等价 "FeedbackGainsDesignModel" 用于反馈增益设计的模型 "FeedbackGainsModel" 模型 gm 或 {gm1,gm2} "FeedbackInputs" sys 的对反馈的输入 uf "InputModel" 输入模型 sys "InputCount" sys 的输入 u 的数量 "MeasuredOutputs" sys 的测量输出 ym "OpenLoopPoles" 泰勒线性化 sys 的极点 "OutputCount" sys 的输出 y 的数量 "SamplingPeriod" sys 的取样周期 "StateEstimatorModel" 模型 sem "StateOutputEstimatorModel" 模型 soem "StateCount" sys 的状态 x 的数量 "TrackedOutputs" sys 的被跟踪的输出 yt - cspec 的可能密钥包括::
-
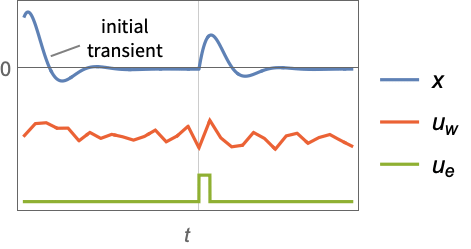
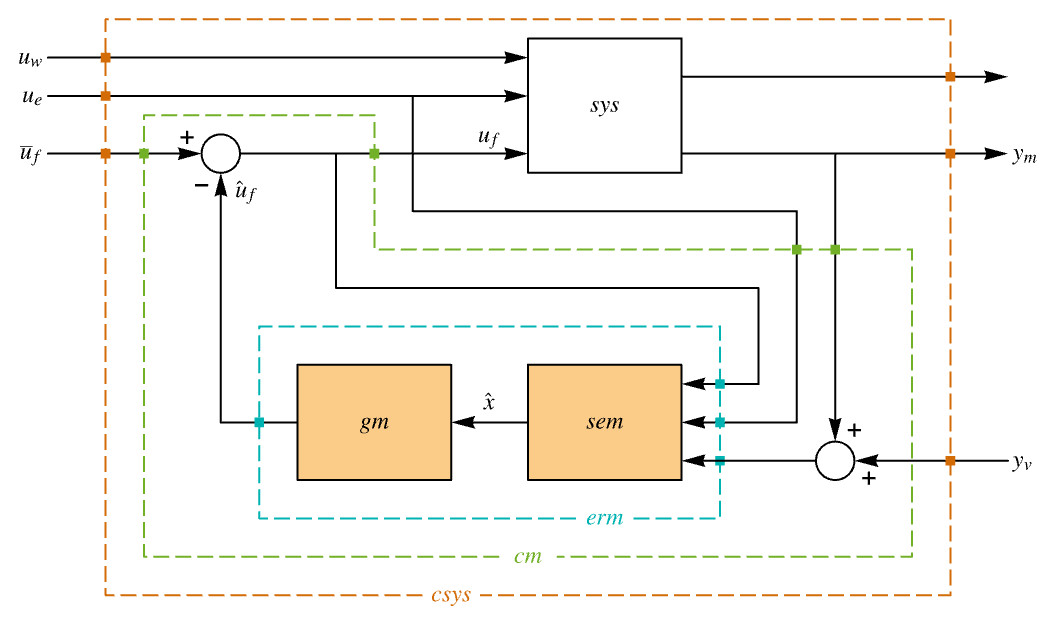
"InputModel" csys 中的输入模型 "Merge" 是否合并 csys "ModelName" csys 的名称 - 调节器布局图.
- 跟踪器布局图.



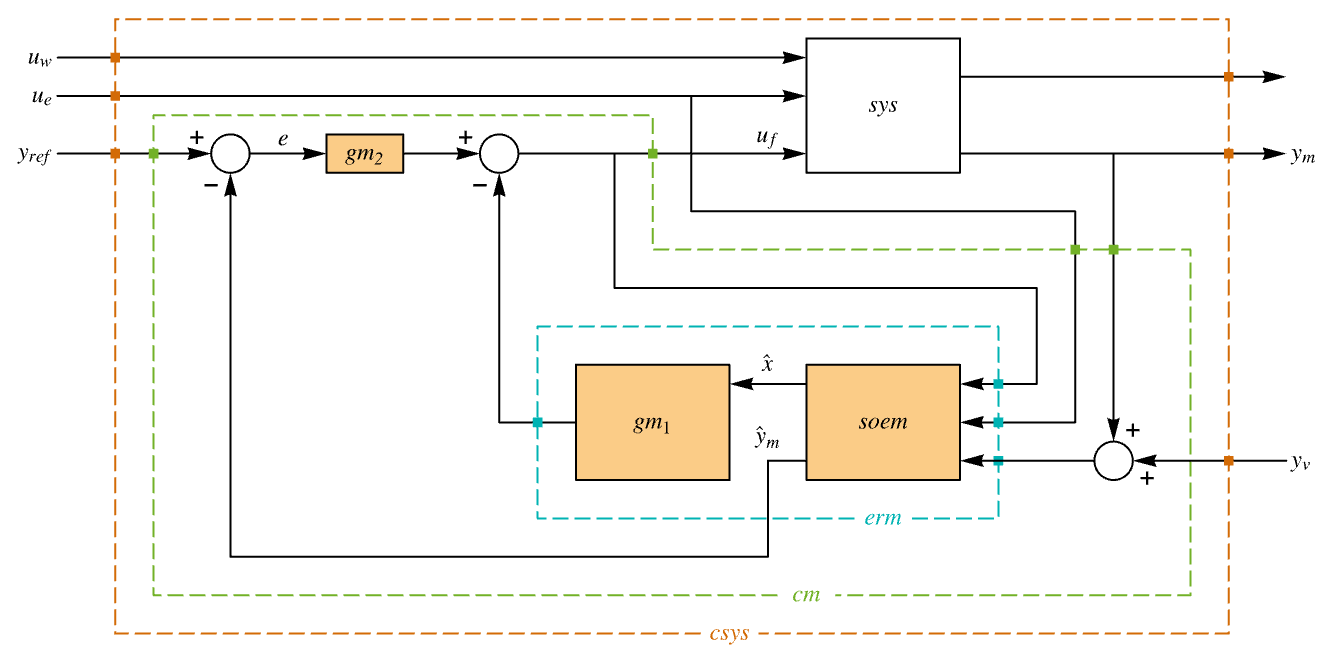
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (33)
基本用途 (4)
受控对象模型 (7)
属性 (14)
默认情况下,LQGRegulator 返回包括估值器和调节器的控制器:
组装 LQGRegulator:
LQGRegulator 模型:
跟踪 (5)
闭环系统 (3)
使用 LQGRegulator 组装受控对象的合并闭环:
属性和关系 (8)
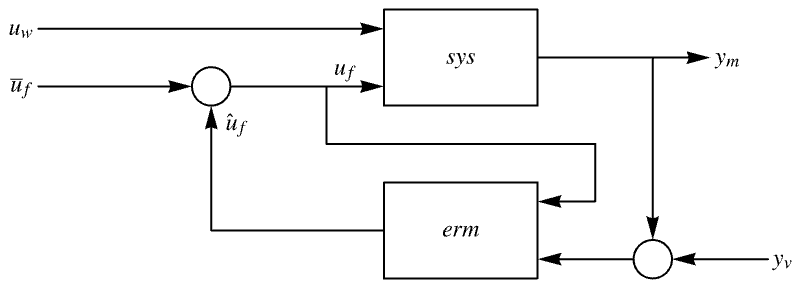
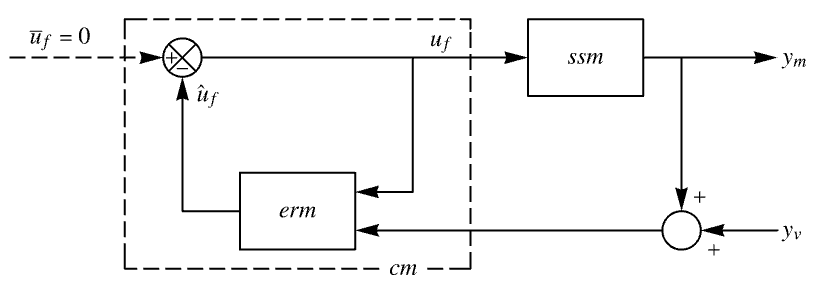
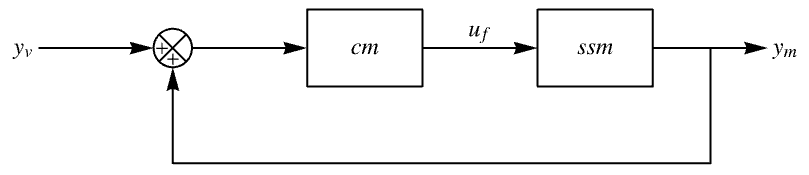
LQGRegulator 可以使用 EstimatorRegulator 进行组装:
使用 EstimatorRegulator 组装 LQGRegulator:
LQGRegulator 给出相同的结果:
LQGRegulator 给出相同的结果:
Wolfram Research (2010),LQGRegulator,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LQGRegulator.html (更新于 2023 年).
文本
Wolfram Research (2010),LQGRegulator,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LQGRegulator.html (更新于 2023 年).
CMS
Wolfram 语言. 2010. "LQGRegulator." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2023. https://reference.wolfram.com/language/ref/LQGRegulator.html.
APA
Wolfram 语言. (2010). LQGRegulator. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LQGRegulator.html 年