LameS
LameS[ν,j,z,m]
次数 ![]() の
の ![]()
![]() 番目のLamé関数
番目のLamé関数 ![]() を楕円パラメータ
を楕円パラメータ ![]() で与える.
で与える.
詳細

- LameSは関数のLaméクラスに属し,楕円座標および球座標のラプラス方程式についての境界値問題を解く.この関数は,数理物理学や量子力学の他の問題にも出現する.
- 記号操作と数値操作の両方に適した数学関数である.
- LameS[ν,j,z,m]はLamé微分方程式
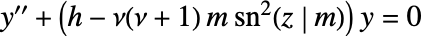 を満足する.ただし,Lamé固有値
を満足する.ただし,Lamé固有値 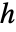 はLameEigenvalueB[ν,j,m]で与えられ,
はLameEigenvalueB[ν,j,m]で与えられ,![TemplateBox[{z, m}, JacobiSN] TemplateBox[{z, m}, JacobiSN]](Files/LameS.ja/8.png) はヤコビ楕円関数JacobiSN[z,m]である.
はヤコビ楕円関数JacobiSN[z,m]である. - LameSを特定の特別な引数について評価すると自動的に厳密値になる.
- LameSは任意の複素引数について任意の数値精度で評価できる.
- LameSは自動的にリストに縫い込まれる.
-
LameS[ν,j,z,0]=Sin[j(
 -z)]
-z)]
- HeunGのパラメータが
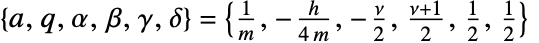 に特化されているなら,LameS[ν,j,z,m]はHeunG[a,q,α,β,γ,δ,ξ]に比例する.ただし,
に特化されているなら,LameS[ν,j,z,m]はHeunG[a,q,α,β,γ,δ,ξ]に比例する.ただし,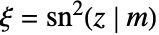 である.
である.
例題
すべて開くすべて閉じるスコープ (27)
可視化 (6)
関数の特性 (2)
微分 (3)
関数表現 (2)
アプリケーション (1)
h=LameEigenvalueB[ν,j,m]のとき,LameSはLamé微分方程式を解く:
特性と関係 (2)
Wolfram Research (2020), LameS, Wolfram言語関数, https://reference.wolfram.com/language/ref/LameS.html.
テキスト
Wolfram Research (2020), LameS, Wolfram言語関数, https://reference.wolfram.com/language/ref/LameS.html.
CMS
Wolfram Language. 2020. "LameS." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LameS.html.
APA
Wolfram Language. (2020). LameS. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LameS.html