LatticeData
LatticeData[lattice,"property"]
gives the specified property for a lattice.
LatticeData[n]
gives a list of named lattices of dimension n.
Details



- Lattices can be specified by standard names such as "FaceCenteredCubic" and "CoxeterTodd".
- LatticeData[] gives a list of classical named lattices.
- LatticeData[patt] gives a list of all named lattices that match the string pattern patt.
- LatticeData[{"type",id},…] gives data for the lattice of the specified type with identifier id.
- Type-related lattices include:
-
{"BarnesWall",n} Barnes–Wall lattice BWn {"Bravais",{"system","centering"}} Bravais lattice for the specified crystal system {"CoxeterBarnes", {r, n}} Coxeter–Barnes lattice 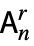
{"DualRootLattice",group} dual root lattice for the specified Lie group {"IntegerLattice",n} integer lattice 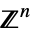
{"KappaLattice",{m,n}} 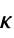 -lattice
-lattice{"LaminatedLattice",{m,n}} laminated lattice 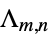
{"MordellWeil",n} Mordell–Weil lattice 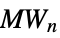
{"Niemeier",n} 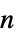
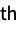 Niemeier lattice
Niemeier lattice{"PerfectLattice",n} perfect lattice {"Quebbemann",n} Quebbemann lattice 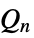
{"RootLattice",group} root lattice for the specified Lie group - Crystal systems are specified by standard names such as "Trigonal", "Monoclinic", etc. Centering is "FaceCentered", "BodyCentered", or "BaseCentered".
- Groups can be specified either for example as "A5" or {"A",5}.
- LatticeData[group,…] is equivalent to LatticeData[{"RootLattice",group},…].
- LatticeData["Properties"] gives a list of possible properties for lattices.
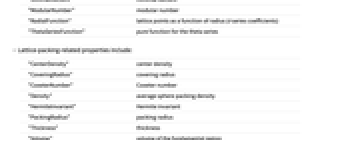
- Lattice points properties include:
-
"Basis" basis vectors "Determinant" determinant of Gram matrix "Dimension" dimension of lattice "Dual" dual lattice "GeneratorMatrix" matrix of generators "Genus" genus of lattice "GlueVectors" glue vectors (when applicable) "GramMatrix" Gram matrix "Image" configuration of points (when applicable) "KissingNumber" kissing number "MinimalNorm" minimal norm "MinimalVectors" minimal vectors "ModularNumber" modular number "RadialFunction" lattice points as a function of radius ( 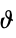 series coefficients)
series coefficients)"ThetaSeriesFunction" pure function for the theta series - Lattice-packing-related properties include:
-
"CenterDensity" center density "CoveringRadius" covering radius "CoxeterNumber" Coxeter number "Density" average sphere packing density "HermiteInvariant" Hermite invariant "PackingRadius" packing radius "Thickness" thickness "Volume" volume of the fundamental region - Other properties include:
-
"QuadraticForm" quadratic form "AutomorphismGroupOrder" order of the automorphism group - Naming-related properties include:
-
"AlternateNames" alternate English names "Name" English name "Notation" standard notation for display "StandardName" Wolfram Language name - LatticeData[lattice,"Classes"] gives a list of the classes in which lattice occurs.
- LatticeData["class"] gives a list of named lattices in the specified class.
- LatticeData[lattice,"class"] gives True or False depending on whether lattice is in the specified class.
- Basic classes of lattices include:
-
"Even" even "Extremal" extremal "Integral" integral "Odd" odd lattice "Unimodular" unimodular - Negative classes of lattices include:
-
"Nonextremal" not extremal "Nonintegral" not integral "Nonunimodular" not unimodular - Using LatticeData may require internet connectivity.
Examples
open allclose allBasic Examples (3)
Scope (24)
Names and Classes (15)
Obtain a list of classical named lattices, including non-lattice packings:
A lattice can be specified by its standard Wolfram Language name:
A Barnes–Wall lattice ![]() is specified by {"BarnesWall",n}:
is specified by {"BarnesWall",n}:
Bravais lattices can be specified by a crystal system with a lattice centering:
Short string forms can be used for root lattices:
Find the English name of a lattice:
A list of alternate names can also be found:
Find the list of named lattices belonging to a class:
Test whether a lattice belongs to a class:
Properties (4)
Property Values (5)
A property value can be any valid Wolfram Language expression:
For the property "ThetaSeriesFunction", lattice data is given as pure functions:
A property that is not applicable to a lattice has the value Missing["NotApplicable"]:
A property that is not available for a lattice has the value Missing["NotAvailable"]:
Generalizations & Extensions (1)
LatticeData works on nonlattice structures such as tetrahedral packings:
Applications (3)
Possible Issues (2)
The generator matrix of a lattice may be given as a SparseArray:
Use Normal to convert to a matrix expression:
Extra coordinates may be used to describe an n-dimensional lattice:
Text
Wolfram Research (2007), LatticeData, Wolfram Language function, https://reference.wolfram.com/language/ref/LatticeData.html.
CMS
Wolfram Language. 2007. "LatticeData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LatticeData.html.
APA
Wolfram Language. (2007). LatticeData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LatticeData.html