WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

LinearRecurrence[ker,init,n]

カーネル ker で初期値 init から始めた線形回帰を反復して得られた長さ n の文字列を与える．

LinearRecurrence[ker,init,{n}]

第 n 項を与える．

LinearRecurrence[ker,init,{nmin,nmax}]

nmin項からnmax項までを与える．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
一般化と拡張  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
関連するガイド
関連リンク
履歴
引用書式

LinearRecurrence

LinearRecurrence[ker,init,n]

カーネル ker で初期値 init から始めた線形回帰を反復して得られた長さ n の文字列を与える．

LinearRecurrence[ker,init,{n}]

第 n 項を与える．

LinearRecurrence[ker,init,{nmin,nmax}]

nmin項からnmax項までを与える．

詳細

  • ker と init は配列だけではなく任意の記号式も含むことができる．
  • 最初のリスト init は少なくともカーネルのリスト ker と同じ長さでなければならない．
  • init が ker よりも長い場合は，最後のLength[ker]要素だけが使われる．
  • LinearRecurrence[{a1,…,ad},{y1,…,yd},n]は初期条件 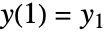, …, 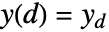で再帰方程式 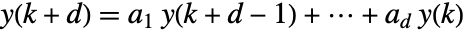を反復させる．
  • 係数 aiと初期値 yjが配列の場合，反復する再帰は値と反転された係数のドット積を伴う 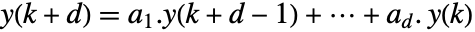と解釈される．
  • 初期値 yjの次元が{m1,…,ms}である場合，係数 aiはスカラーであるか，さもなければ次元{m1,m1}でなければならない．

例題

すべて開く すべて閉じる

例  (3)

Wolfram Language code: LinearRecurrence[{a, b}, {1, 1}, 5]

カーネル{-3, 1}で一階差分方程式の初期値問題を解く：

Wolfram Language code: LinearRecurrence[{-3, 1}, {7, 2}, 10]

フィボナッチ(Fibonacci)数の最初の数個を求める：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, 10]
Wolfram Language code: Table[Fibonacci[n], {n, 10}]

スコープ  (2)

LinearRecurrenceは記号カーネルと初期値に使うことができる：

Wolfram Language code: LinearRecurrence[{a, b}, {c, d}, 5]

LinearRecurrenceは配列に使うことができる：

Wolfram Language code: LinearRecurrence[{1, 1}, {{1, 2}, {2, 1}}, 10]
Wolfram Language code: LinearRecurrence[{{{1, 1}, {0, 1}}, {{1, 0}, {-1, 1}}}, {{1, 2}, {2, 1}}, 6]

一般化と拡張  (2)

与えられた範囲から値のサブセットを生成する：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {-5, 5}]

反復の最後の値だけを得る：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {5, 5}]

アプリケーション  (2)

パドヴァン(Padovan)数列を含む再帰数列を生成する：

Wolfram Language code: LinearRecurrence[{0, 1, 1}, {1, 1, 1}, 10]

ペル(Pell)数：

Wolfram Language code: LinearRecurrence[{2, 1}, {0, 1}, 10]

ペル・リュカ(Pell–Lucas)数：

Wolfram Language code: LinearRecurrence[{2, 1}, {2, 2}, 10]

ペリン(Perrin)数列：

Wolfram Language code: LinearRecurrence[{0, 1, 1}, {3, 0, 2}, 10]

大きい n についての線形回帰の第 n 項を効率的に計算する：

Wolfram Language code: LinearRecurrence[{3, 2, 1, 4}, {1, -36, 9, 80}, {500}]//AbsoluteTiming
Wolfram Language code: LinearRecurrence[{3, 2, 1, 4}, {1, -36, 9, 80}, {500000}];//AbsoluteTiming

特性と関係  (1)

RSolveは差分方程式の記号解を求める：

Wolfram Language code: RSolve[{a[n + 2] == a[n + 1] + a[n], a[0] == 1, a[1] == 1}, a, n]
Wolfram Language code: Table[a[n] /. %[[1]], {n, 0, 6}]

LinearRecurrenceは手続き型の解を生成する：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1}, {7}]

RSolveValueを使って同じ結果を得る：

Wolfram Language code: RSolveValue[{a[n + 2] == a[n + 1] + a[n], a[0] == 1, a[1] == 1}, a[6], n]

考えられる問題  (1)

初期値はカーネルより長い：

Wolfram Language code: LinearRecurrence[{1, 1}, {1, 1, a, b}, 10]

末尾の項だけが使われる：

Wolfram Language code: LinearRecurrence[{1, 1}, {a, b}, {5, 10}]

おもしろい例題  (1)

Wolfram Language code: ListLinePlot[{Re[#], Im[#]}& /@ LinearRecurrence[{Exp[I Pi / Sqrt[2]], I} / 1.1, {1, 1}, 100], PlotRange -> All, AspectRatio -> Automatic]
Wolfram Research (2008), LinearRecurrence, Wolfram言語関数， https://reference.wolfram.com/language/ref/LinearRecurrence.html （2017年に更新）.

テキスト

Wolfram Research (2008), LinearRecurrence, Wolfram言語関数， https://reference.wolfram.com/language/ref/LinearRecurrence.html （2017年に更新）.

CMS

Wolfram Language. 2008. "LinearRecurrence." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/LinearRecurrence.html.

APA

Wolfram Language. (2008). LinearRecurrence. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearRecurrence.html

BibTeX

@misc{reference.wolfram_2026_linearrecurrence, author="Wolfram Research", title="{LinearRecurrence}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/LinearRecurrence.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_linearrecurrence, organization={Wolfram Research}, title={LinearRecurrence}, year={2017}, url={https://reference.wolfram.com/language/ref/LinearRecurrence.html}, note=[Accessed: 02-November-2026]}