MagnetostaticPDEComponent
MagnetostaticPDEComponent[vars,pars]
yields a current-free magnetostatic PDE term with variables vars and pars.
Details



- MagnetostaticPDEComponent is typically used to generate a magnetostatic equation for permanent magnets with model variables vars and model parameters pars.
- MagnetostaticPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- MagnetostaticPDEComponent models static magnetic fields produced by permanent magnets and other current-free magnetic sources.
- MagnetostaticPDEComponent models magnetostatic phenomena with the dependent variable
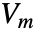 and the magnetic scalar potential.
and the magnetic scalar potential. 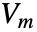 is in units of amperes [
is in units of amperes [![TemplateBox[{InterpretationBox[, 1], "A", amperes, "Amperes"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "A", amperes, "Amperes"}, QuantityTF]](Files/MagnetostaticPDEComponent.en/4.png) ], independent variables
], independent variables 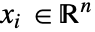 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagnetostaticPDEComponent.en/6.png) ].
]. - Stationary variables vars are vars={Vm[x1,…,xn],{x1,…,xn}}.
- MagnetostaticPDEComponent generally does not produces a time-dependent PDE.
- To model permanent magnets, the MagnetostaticPDEComponent equation is given as:
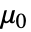 is the vacuum permeability in units of [
is the vacuum permeability in units of [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/9.png) ] and
] and 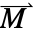 the magnetization vector in units of [
the magnetization vector in units of [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/11.png) ].
].- The magnetization vector
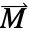 specifies the magnetic dipole moment per unit volume within a material, indicating the strength and direction of its magnetic properties.
specifies the magnetic dipole moment per unit volume within a material, indicating the strength and direction of its magnetic properties. - An alternative to the magnetization vector
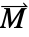 , is the remanent magnetic flux density vector
, is the remanent magnetic flux density vector 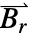 in units of [
in units of [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/15.png) ]. The MagnetostaticPDEComponent equation is given as:
]. The MagnetostaticPDEComponent equation is given as: 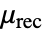 is the unitless recoil permeability.
is the unitless recoil permeability.- For linear materials, like iron, the MagnetostaticPDEComponent equation simplifies to:
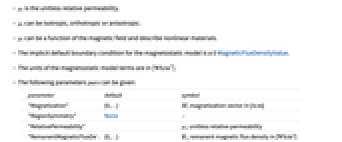
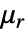 is the unitless relative permeability.
is the unitless relative permeability.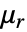 can be isotropic, orthotropic or anisotropic.
can be isotropic, orthotropic or anisotropic.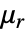 can be a function of the magnetic field and describe nonlinear materials.
can be a function of the magnetic field and describe nonlinear materials.- The implicit default boundary condition for the magnetostatic model is a 0 MagneticFluxDensityValue.
- The units of the magnetostatic model terms are in [
![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 3}}, webers per meter cubed, {{(, "Webers", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 3}}, webers per meter cubed, {{(, "Webers", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/22.png) ].
]. - The following parameters pars can be given:
-
parameter default symbol "Magnetization" {0,…} 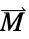 , magnetization vector in [
, magnetization vector in [![TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"A", , "/", , "m"}, amperes per meter, {{(, "Amperes", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/24.png) ]
]"RegionSymmetry" None 
"RelativePermeability" 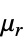 , unitless relative permeability
, unitless relative permeability
"RemanentMagneticFluxDensity" {0,…} 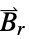 , remanent magnetic flux density in [
, remanent magnetic flux density in [![TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"Wb", , "/", , {"m", ^, 2}}, webers per meter squared, {{(, "Webers", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/28.png) ]
]"Thickness" 1 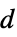 , thickness in [
, thickness in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MagnetostaticPDEComponent.en/30.png) ]
] "VacuumPermeability" 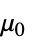
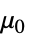 , vacuum permeability in [
, vacuum permeability in [![TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"H", , "/", , "m"}, henries per meter, {{(, "Henries", )}, /, {(, "Meters", )}}}, QuantityTF]](Files/MagnetostaticPDEComponent.en/33.png) ]
] - All parameters may depend on the spatial variable
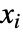 and dependent variable
and dependent variable 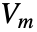 .
. - The number of independent variables
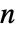 determines the dimensions of
determines the dimensions of 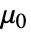 or
or 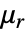 and the length of vectors
and the length of vectors 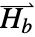 ,
, 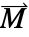 and
and 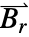 .
. - The models are available in a 2D, a 2D axisymmetric and a 3D form.
- A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction equation 2D 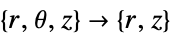
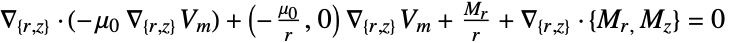
- In 2D, when a "Thickness"
 is specified, the MagnetostaticPDEComponent equation is given as:
is specified, the MagnetostaticPDEComponent equation is given as: - The input specification for the parameters is exactly the same as for their corresponding operator terms.
- If no parameters are specified, the default magnetostatic PDE is:
- If the MagnetostaticPDEComponent depends on parameters
 that are specified in the association pars as …,keypi…,pivi,…], the parameters
that are specified in the association pars as …,keypi…,pivi,…], the parameters 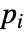 are replaced with
are replaced with 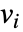 .
.
Examples
open allclose allBasic Examples (3)
Define a default magnetostatic PDE model:
Set up a magnetostatic model with particular material parameters:
To model a permanent magnet in 2D with a rectangular cross section, define the mesh to use:
Visualize the internal boundaries of the magnet region:
Solve the magnetostatic PDE model with a magnet transversely magnetized in the direction of the ![]() axis:
axis:
Scope (3)
Applications (1)
To model a 3D cylinder permanent magnet, set up variables:
Define the magnet region of height ![]() [
[![]() ] and radius
] and radius ![]() [
[![]() ]:
]:
Define the magnetization vector:
Set up the mesh with a sphere of air of ![]() [
[![]() ] that represents the surrounding volume:
] that represents the surrounding volume:
Visualize the magnet cylinder that is inside the mesh:
Text
Wolfram Research (2025), MagnetostaticPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/MagnetostaticPDEComponent.html.
CMS
Wolfram Language. 2025. "MagnetostaticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MagnetostaticPDEComponent.html.
APA
Wolfram Language. (2025). MagnetostaticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MagnetostaticPDEComponent.html