MandelbrotSetIterationCount

MandelbrotSetIterationCount[c]

c がマンデルブロ(Mandelbrot)集合に含まれるかどうかを見極めるための，から始めた関数 の反復回数を返す．

詳細とオプション

  • マンデルブロ集合とは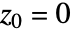，から始めた場合に，数列 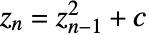が無限大に発散しないすべての複素数 c の集合である．
  • オプション設定をMaxIterations->n とすると，数列 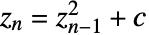は，発散するかどうかを見極めるために，最高で n 回反復される．
  • デフォルト設定はMaxIterations->1000である．
  • 最大反復回数に達した場合，z はマンデルブロ集合に含まれると解釈される．
  • マンデルブロ集合に含まれることが前もってアルゴリズムにとって既知である点については，MandelbrotSetIterationCountはMaxIterationsの値より1大きい数を返す．

例題

すべて開くすべて閉じる

例  (4)

がマンデルブロ集合に含まれないことが分かるまでに，何回の反復が必要かを求める：

ゼロはマンデルブロ集合に含まれることが分かっているため，が返される：

0.2501がマンデルブロ集合に含まれないと分かるまでに，さらに数回の反復が必要である：

MandelbrotSetIterationCountは，あらゆる種類の数に使うことができる：

オプション  (2)

MaxIterations  (1)

真の反復回数を求めるためにMaxIterationsを大きくする必要があることがある：

WorkingPrecision  (1)

WorkingPrecisionを大きくすることでより正確な結果が与えられることがある：

特性と関係  (1)

MandelbrotSetIterationCountに適用されたArrayPlotは，事実上MandelbrotSetPlotである：

考えられる問題  (1)

MaxIterations->Infinityとすると，有限ステップ数では計算が収束しないことがある：

はマンデルブロ集合であることが分かっているので，これはDirectedInfinityを返す：

おもしろい例題  (3)

反復回数のHistogramを虚軸に沿って作る：

反復回数を高さとして表示する：

回転されたマンデルブロ集合の半分：

Wolfram Research (2014), MandelbrotSetIterationCount, Wolfram言語関数， https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

テキスト

Wolfram Research (2014), MandelbrotSetIterationCount, Wolfram言語関数， https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

CMS

Wolfram Language. 2014. "MandelbrotSetIterationCount." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

APA

Wolfram Language. (2014). MandelbrotSetIterationCount. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html

BibTeX

@misc{reference.wolfram_2024_mandelbrotsetiterationcount, author="Wolfram Research", title="{MandelbrotSetIterationCount}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mandelbrotsetiterationcount, organization={Wolfram Research}, title={MandelbrotSetIterationCount}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html}, note=[Accessed: 21-November-2024 ]}