MandelbrotSetIterationCount

MandelbrotSetIterationCount[c]

从 开始，返回用来决定 c 是否在曼德博集合（Mandelbrot set）内的函数 的迭代次数.

更多信息和选项

  • 曼德博集合是所有复数 c 的集合，这些 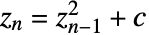c 使得数列 当从 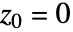开始时不会发散于无穷大.
  • 若设置 MaxIterations->n，则数列 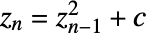为确定其是否发散最多迭代 n 次.
  • 默认设置为 MaxIterations->1000.
  • 如果达到了迭代次数的最大值，则 z 应在曼德博集合中.
  • 对于某些算法能提前判断出在曼德博集合中的点，MandelbrotSetIterationCount 会返回一个大于 MaxIterations 的值.

范例

打开所有单元关闭所有单元

基本范例  (4)

求出需要用来确定 不在曼德博集合内的迭代次数：

由于已知零在曼德博集合内，所以返回 ：

要确定0.250001不在曼德博集合内，需要多迭代几次：

MandelbrotSetIterationCount 可用于所有类型的数字：

选项  (2)

MaxIterations  (1)

有时候需要提高 MaxIterations 的值，才能得到迭代的真实数值：

WorkingPrecision  (1)

有时候提高 WorkingPrecision 的值，可以得到一个更精确的结果：

属性和关系  (1)

ArrayPlot 应用于 MandelbrotSetIterationCount 本质上就是 MandelbrotSetPlot：

可能存在的问题  (1)

设置 MaxIterations->Infinity，计算可能不会再有限数目的步骤中收敛：

由于知道 是在曼德博集合内的，则返回 DirectedInfinity：

巧妙范例  (3)

制作一张沿着虚轴迭代的次数直方图 Histogram：

将迭代次数表示为高度：

一个旋转曼德博集合的一半：

Wolfram Research (2014)，MandelbrotSetIterationCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

文本

Wolfram Research (2014)，MandelbrotSetIterationCount，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

CMS

Wolfram 语言. 2014. "MandelbrotSetIterationCount." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html.

APA

Wolfram 语言. (2014). MandelbrotSetIterationCount. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html 年

BibTeX

@misc{reference.wolfram_2024_mandelbrotsetiterationcount, author="Wolfram Research", title="{MandelbrotSetIterationCount}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mandelbrotsetiterationcount, organization={Wolfram Research}, title={MandelbrotSetIterationCount}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetIterationCount.html}, note=[Accessed: 21-November-2024 ]}