NDEigenvalues

NDEigenvalues[ℒ[u[x,y,…]],u,{x,y,…}∈Ω,n]

領域 Ω 上での線形微分演算子 ℒ についての n 個の最小固有値を与える．

NDEigenvalues[{ℒ1[u[x,y,…],v[x,y,…],…],ℒ2[u[x,y,…],v[x,y,…],…],…},{u,v,…},{x,y,…}∈Ω,n]

領域 Ω 上での連結微分演算子{op1,op2,…}についての固有値を与える．

NDEigenvalues[eqns,{u,…},t,{x,y,…}∈Ω,n]

連結された時間依存微分方程式 eqns の解 u,… についての空間変数{x,y,…}内の固有値を与える．

詳細とオプション

  • NDEigenvaluesは，固有モードソルバとしても知られているが，微分方程式の固有値を領域上で求める数値固有ソルバである．
  • NDEigenvaluesは，n 個の最小の固有値 λiのリスト{λ1,…,λn}を与える．
  • 方程式 eqns aはNDSolveにおけるように指定される．
  • 固有値は絶対値の昇順に並べられる．
  • 同次DirichletCondition，NeumannValueあるいは一般化されたロビン(Robin)の各境界条件が含まれることがある． »
  • PeriodicBoundaryConditionが含まれることがある．
  • 境界 ∂Ωの一部で境界条件が指定されていない場合，これはノイマン零条件を指定してあることに等しい．
  • 時間依存一次方程式の系については，時間微分D[u[t,x,y,…],t],D[v[t,x,y,…],t],…は事実上 λ u[x,y,…],λ v[x,y,…],…で置換される．
  • 一次より高い時間依存方程式の系は，媒介変数 ut=u*,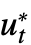=…, vt=v*,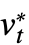=…, …を持つ連結された一次の系に簡約される．関数 u, v, …のみが返される． »
  • NDEigenvaluesは，解のさまざまなステージを制御することがあるMethodオプションを取る．Method->{s1->m1,s2->m2,…}のとき，ステージ siはメソッド miで制御される．ステージが明示的に与えられない場合は，NDEigenvaluesは与えられたメソッドをどのステージに適用するかを自動的に決定しようとする．
  • 可能な解のステージ
  • "PDEDiscretization"空間演算子の離散化
    "Eigensystem"離散化された系からの固有系の計算
    "VectorNormalization"固有関数の構築に使われる固有ベクトルの正規化

例題

すべて開くすべて閉じる

例  (3)

[0,π]についてのラプラス演算子の最小の4つの固有値を求める：

辺が固定された円形膜の最初の6つの固有値を計算する：

シュレディンガー(Schrödinger)演算子をパラメータ ，ポテンシャル で指定する：

小さい方から5つの固有値を求める：

スコープ  (12)

1D  (7)

ラプラス演算子を指定する：

同次ディリクレ(Dirichlet)境界条件を指定する：

最小の4つの固有値を求める：

ラプラス演算子を指定する：

同次ノイマン境界条件を指定する：

最も小さい4つの固有値を求める：

次は等しい：

同次ディリクレ境界条件を持つ一過式を指定する：

4つの最小固有値を求める：

同次ディリクレ境界条件を持つ波動方程式を指定する：

4つの最小固有値を求める：

一般化された波動方程式 の固有値を計算する：

等価な常微分方程式の一次系の厳密解と比較する：

リウヴィル演算子を指定する：

4つの最小固有値を計算する：

解析的固有値を持つ固有値と比較する：

ラプラス演算子のパラメトリック複素数値周期固有値を計算する関数を書く：

固有値を求める：

0から4 までの範囲で固有値を可視化する：

2D  (5)

ラプラス演算子を指定する：

4つの最小固有値を求める：

ラプラス演算子を指定する：

単位円板上の演算子の4つの最小固有値を求める：

同次ディリクレ境界条件を持つラプラス演算子を指定する：

長方形内の9つの最小固有値を求める：

同次ディリクレ境界条件を持つ波動方程式を指定する：

円板内の4つの最小固有値を求める：

部分的に制約された固有値問題を解く：

オプション  (6)

Method  (6)

"Eigensystem"  (4)

固有値を求めるために使うメソッドを指定する：

この場合は，デフォルトメソッドの方が速い：

デフォルトメソッドとしてアーノルディ法が使われる：

アーノルディ法についての最大反復回数を指定する：

Sturm–Liouville演算子の2つの固有値を，EigenvaluesのためのFEASTメソッドでの範囲で求める：

Sturm–Liouville理論によると，固有値は他と異ならなければならないが，この例では2つは縮退に近い：

区間の端点はFEASTが固有値を求める区間には含まれない．より詳しい情報は，Eigenvaluesの関数ページを参照のこと．

"Shift"オプションの使い方は以下の例で説明されている．

"PDEDiscretization"  (1)

もとになる計算についてのMaxCellMeasureを変更する：

厳密な固有値は0,1,4,9,…であるので，固有値誤差は以下の通りである：

より細かいメッシュだと離散化誤差が小さくなる：

"VectorNormalization"  (1)

計算された固有値を正規化せずに計算する：

正規化は固有値には影響しない：

アプリケーション  (4)

音響  (1)

Miniの断面の近似値の音響固有値と固有関数を計算する．断面の画像をインポートする：

マスクツールを使って境界グラフィックスを作成する：

グラフィックスを離散化する：

断面の6つの固有値を計算する：

構造力学  (1)

平面応力の偏微分方程式を指定する：

制約固有値を計算する：

固有値と固有関数の間隔  (1)

区間における固有値を求める：

量子力学  (1)

シュレディンガー演算子をパラメータ ，ポテンシャル で指定する：

細分化されたメッシュ上で小さい方から10個の固有値を求める：

特性と関係  (3)

同次ディリクレ境界条件を持つ過渡方程式を指定する：

最小固有値を4個求める：

これは，以下と等価である：

高次時間依存偏微分方程式の解析解を比較する．

が0から までの範囲の波動方程式 の6つの最小固有値を求める：

の厳密解が2つの一次方程式の系に変換された固有値を比較する：

高次時間依存偏微分方程式と一次偏微分方程式の系の間の関係を示す．

0から までの範囲の波動方程式 の最も小さい6つの固有値を求める：

一次偏微分方程式の系として与えられる波動方程式の最も小さい6つの固有値を求める：

二次の系についての固有値と一次方程式の系についての固有値は等しい：

考えられる問題  (10)

計算された固有値は離散化の粒度に依存する：

厳密な固有値は0,1,4,9,…なので，固有値誤差は以下の通りである：

メッシュをより細かくすると離散化誤差が小さくなる：

波動方程式の固有値は角周波数の平方根である：

等価な常微分方程式の一次の系の厳密解と比較する：

非同次ディリクレ条件のある固有値は解くことができない：

同次ディリクレ条件のある固有値は解くことができる：

非同次ノイマン値のある固有値は解くことができない：

同次ノイマン値のある固有値は解くことができる：

同じ結果：

一般化された非同次ノイマン値のある固有値は解くことができない：

演算子と可能な境界条件は定常で線形である必要がある：

初期条件は0に設定され，無視される：

同じ結果：

NDEigenvalueはPDEを時間依存のPDEに変換する．この変換は一意的ではなく，対になったPDEについては予想外の結果になるかもしれない：

内部的に，与えられた方程式は時間依存のPDEに書き換えられる．前の場合の与えられた従属変数{v[x],u[x]}から次の時間系{D[v[t, x], t] == - u[t, x] - Laplacian[u[t, x], {x}],D[u[t, x], t] == -v[t, x] - Laplacian[v[t, x], {x}]}が生成される：

方程式系を一意的に指定するためには，時間的記述を使うのが最もよい：

このテーマについての詳細情報は有限要素法の使用上のヒントを参照されたい．

NDEigenvaluesは，場合によっては，一対の偏微分方式に対しては予期されないと思われる結果を返すことがある：

この問題を回避する方法の一つに，"InterpolationOrder"オプションを使って従属変数の順序を指定することが考えられる：

"Direct"メソッドを使うこともできる：

このトピックについては有限要素法の使用上のヒントも参照されたい．

NDEigenvaluesは，与えられた線形微分演算子について，最も小さい 個の固有値を求める．特に，例えば，多くの量子力学的問題におけるように，最も負の固有値を見付けることに興味がある場合は，最も負の 個の固有値がNDEigenvaluesがデフォルトで返す 個の固有値と一致しない可能性がある．これを理解するために以下の例について考える．

例として，水素原子についての無次元動径シュレディンガー(Schrödinger)方程式を取り上げる．ここでは，エネルギー単位はリュードベリ(Rydberg)で，長さはボーア(Bohr)半径で計測される．

動径シュレディンガー方程式を定義する：

固有値問題を について解く．近似の品質を向上させるために細分化メッシュを使用する：

電子ボルトで取得された固有値を見る：

これらはに最も近い固有値に対応する．しかし，望ましい順序ではない．例として，この問題の解析的固有値を見ることにする．

この方程式の解析的エネルギーは以下の関係に従う：

この固有値の下限が，例えば であると事前に分かっていれば，固有値問題 を として再定義できる．言い換えるなら，次のように新たな固有値問題とすることができる．，ただし かつ ．は についての負の下限なので，このシフトによって が正の値のみを取ることが保証される．したがって，最も小さい 個の の値は最も負である の 個の値に対応する．このように， について計算して を得ることができる．これを行う最も簡単な方法は"Shift"オプションを使うことである．

下限を設定する：

シフトを定義して固有値問題を解く：

電子ボルトで入手された固有値を見る：

これらは最も負である固有値に対応する．しかし，順序は逆順であり，固有状態をソートし直す必要がある．

Sortを使って固有状態をソートする：

解析的固有値と入手された結果の違いを見る：

Wolfram Research (2015), NDEigenvalues, Wolfram言語関数， https://reference.wolfram.com/language/ref/NDEigenvalues.html.

テキスト

Wolfram Research (2015), NDEigenvalues, Wolfram言語関数， https://reference.wolfram.com/language/ref/NDEigenvalues.html.

CMS

Wolfram Language. 2015. "NDEigenvalues." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NDEigenvalues.html.

APA

Wolfram Language. (2015). NDEigenvalues. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NDEigenvalues.html

BibTeX

@misc{reference.wolfram_2024_ndeigenvalues, author="Wolfram Research", title="{NDEigenvalues}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/NDEigenvalues.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ndeigenvalues, organization={Wolfram Research}, title={NDEigenvalues}, year={2015}, url={https://reference.wolfram.com/language/ref/NDEigenvalues.html}, note=[Accessed: 21-November-2024 ]}