represents the special non-commutative algebra alg.
NonCommutativeAlgebra[spec]
represents the general non-commutative algebra given by the specification spec.


NonCommutativeAlgebra
represents the special non-commutative algebra alg.
NonCommutativeAlgebra[spec]
represents the general non-commutative algebra given by the specification spec.
Details


- NonCommutativeAlgebra is used to represent a non-commutative algebra.
- NonCommutativeAlgebra objects are used to specify the underlying algebra in functions like NonCommutativeExpand, NonCommutativeCollect, NonCommutativeGroebnerBasis, etc.
- Possible special algebras alg include:
-
{Dot,n} 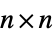 matrices
matricesNonCommutativeMultiply non-commutative polynomials Composition linear endomorphisms with composition TensorProduct infinite direct sum of tensor powers - All special algebras are essentially free algebras that differ only in operation names. No relations between symbolic variables are assumed.
- The specification spec is an association with the following keys and their default values:
-
"Multiplication" NonCommutativeMultiply non-commutative multiplication 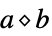
"Addition" Plus addition 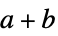
"Unity" 1 one for multiplication 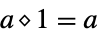 and
and 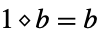
"Zero" 0 zero for addition 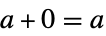 and
and 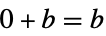
"CommutativeVariables" {} variables that commute with all elements "ScalarVariables" {} scalar variables - The value associated with a given key in a NonCommutativeAlgebra object ncalg can be extracted with ncalg["key"].
- A NonCommutativeAlgebra object represents a unitary algebra. An algebra is a vector space equipped with a bilinear product operation. An algebra is unitary if its product operation has a neutral element.
- "Addition" is assumed to be a commutative operation with "Zero" acting as the zero.
- "Multiplication" is assumed to be bilinear, which means
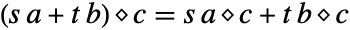 and
and 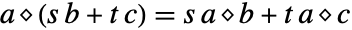 where
where 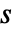 and
and 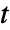 are scalars. Furthermore, "Unity" is acting as the one.
are scalars. Furthermore, "Unity" is acting as the one. - "ScalarVariables" are assumed to be scalars. Scalar addition and multiplication are represented by Plus and Times.
- The detailed specifications spec for the special algebras alg are given below:
-
{Dot,n} <|"Multiplication"Dot, "Unity"SymbolicIdentityArray[{n}],"Zero"SymbolicZerosArray[{n,n}]|> NonCommutativeMultiply <||> Composition <|"Multiplication"Composition, "Unity"Identity|> TensorProduct <|"Multiplication"TensorProduct|>
Examples
open all close allBasic Examples (2)
A NonCommutativeAlgebra object with default properties:
Specify the underlying algebra in NonCommutativeExpand:
Specify multiplication, addition and scalar variables:
Specify the underlying algebra in NonCommutativeExpand:
Scope (5)
Specify that the variable c commutes with all algebra elements:
Square matrices with Dot product form an algebra:
Linear endomorphisms with Composition form an algebra:
Compute with polynomials over an abstract algebra with symbolic property names:
Scalar arguments to algebra operations are interpreted as scalar multiples of the multiplicative unity:
Applications (6)
Check whether two noncommutative polynomials are equal:
Expand the difference of the polynomials:
Simplify an expression involving ![]() matrices
matrices ![]() and
and ![]() :
:
Find the inverses in the expression:
Generate the relations satisfied by the inverses:
Pick a variable order that puts the most complicated variables first:
Compute the Gröbner basis of the ideal generated by the relations over the algebra of ![]() matrices:
matrices:
Reducing the expression modulo the Gröbner basis shows that it is equal to the identity matrix:
Use ArraySimplify to do the above simplification steps automatically:
Prove the Woodbury matrix identity:
In the standard formulation, ![]() is an
is an ![]() matrix,
matrix, ![]() is a
is a ![]() matrix, with
matrix, with ![]() ,
, ![]() is an
is an ![]() matrix, and
matrix, and ![]() is a
is a ![]() matrix. However, by replacing
matrix. However, by replacing ![]() ,
, ![]() and
and ![]() with the block matrices
with the block matrices ![]() ,
, ![]() and
and ![]() , one may assume that all matrices belong to the algebra of
, one may assume that all matrices belong to the algebra of ![]() matrices. It will be shown that the difference of the sides of the identity reduces to zero modulo the Gröbner basis of the ideal generated by relations implied by the properties of the matrix inverse.
matrices. It will be shown that the difference of the sides of the identity reduces to zero modulo the Gröbner basis of the ideal generated by relations implied by the properties of the matrix inverse.
Compute the difference ![]() of the sides of the Woodbury matrix identity:
of the sides of the Woodbury matrix identity:
Generate the relations satisfied by the inverses:
Pick a variable order that puts the most complicated variables first:
Compute the Gröbner basis of the ideal generated by the relations over the algebra of ![]() matrices:
matrices:
Reduce ![]() modulo the Gröbner basis. The result is a zero matrix, which proves the identity:
modulo the Gröbner basis. The result is a zero matrix, which proves the identity:
Use ArraySimplify to do the above simplification steps automatically:
Construct a finitely presented group. The dicyclic group ![]() is given by generators
is given by generators ![]() and relations
and relations ![]() . The group algebra of
. The group algebra of ![]() is given by four generators:
is given by four generators:
The generators satisfy the following relations:
Compute the Gröbner basis of the ideal generated by the relations:
Note that reducing an arbitrary monomial modulo the Gröbner basis gives a monomial that does not contain ![]() and
and ![]() . This shows that reducing an arbitrary monomial in
. This shows that reducing an arbitrary monomial in ![]() and
and ![]() of total degree
of total degree ![]() yields a monomial of a total degree at most
yields a monomial of a total degree at most ![]() :
:
Hence, all elements of the group can be represented as reduced monomials of degree at most ![]() :
:
It has been proven that ![]() is a finite group of order
is a finite group of order ![]() :
:
Compute in the Clifford algebra ![]() . The algebra has six generators:
. The algebra has six generators:
The generators satisfy the following relations:
The set of relations is a Gröbner basis:
Compute the canonical representation of ![]() :
:
Compute the canonical representation of ![]() :
:
Compute in the Weyl algebra associated to the differential ring of bivariate polynomials. The algebra has four generators:
The generators satisfy the following relations:
The set of relations is a Gröbner basis:
Compute the canonical representation of ![]() and
and ![]() :
:
Compute the canonical representation of ![]() :
:
Elements of the Weyl algebra correspond to differential operators with product representing composition:
Verify that the operator corresponding to ![]() is the composition of the operators corresponding to
is the composition of the operators corresponding to ![]() and
and ![]() :
:
Related Guides
History
Text
Wolfram Research (2025), NonCommutativeAlgebra, Wolfram Language function, https://reference.wolfram.com/language/ref/NonCommutativeAlgebra.html.
CMS
Wolfram Language. 2025. "NonCommutativeAlgebra." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NonCommutativeAlgebra.html.
APA
Wolfram Language. (2025). NonCommutativeAlgebra. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NonCommutativeAlgebra.html
BibTeX
@misc{reference.wolfram_2025_noncommutativealgebra, author="Wolfram Research", title="{NonCommutativeAlgebra}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/NonCommutativeAlgebra.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_noncommutativealgebra, organization={Wolfram Research}, title={NonCommutativeAlgebra}, year={2025}, url={https://reference.wolfram.com/language/ref/NonCommutativeAlgebra.html}, note=[Accessed: 15-January-2026]}