OrthogonalMatrix
OrthogonalMatrix[omat]
将正交矩阵 omat 转换为结构化数组.
更多信息和选项


- 当正交矩阵表示为结构化数组时,便于进行指定和更高效地进行运算,包括 Inverse 和 LinearSolve.
- 使用正交矩阵的矩阵分解包括 QR、Hessenberg、Schur 和奇异值分解.
- 对于正交矩阵
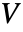 ,列向量
,列向量 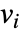 是正交的, 因此
是正交的, 因此 ![v_i.v_j=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq] v_i.v_j=TemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]](Files/OrthogonalMatrix.zh/3.png) .
. - 正交方阵
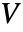 是转置等于其逆矩阵的矩阵;也就是说,它满足关系式
是转置等于其逆矩阵的矩阵;也就是说,它满足关系式 ![TemplateBox[{V}, Transpose]=TemplateBox[{V}, Inverse] TemplateBox[{V}, Transpose]=TemplateBox[{V}, Inverse]](Files/OrthogonalMatrix.zh/6.png) .
. - 正交方阵的逆矩阵也是正交矩阵.
- 在以下情况下,维度为 p×q 矩阵
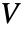 是正交的:如果 p≥q 且
是正交的:如果 p≥q 且 ![TemplateBox[{V}, Transpose]V TemplateBox[{V}, Transpose]V](Files/OrthogonalMatrix.zh/8.png) 是 q×q 的单位矩阵,或 p≤q 且
是 q×q 的单位矩阵,或 p≤q 且 ![VTemplateBox[{V}, Transpose] VTemplateBox[{V}, Transpose]](Files/OrthogonalMatrix.zh/9.png) 是 p×p 的单位矩阵.
是 p×p 的单位矩阵. - 正交矩阵在矩阵乘法下是封闭的,因此
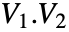 也是正交矩阵.
也是正交矩阵. - 对于 OrthogonalMatrix sa,可通过 sa["prop"] 获取以下属性 "prop":
-
"Matrix" 以完整数组表示的正交矩阵 "Properties" 支持的属性的列表 "Structure" 结构化数组的类型 "StructuredData" 结构化数组存储的内部数据 "StructuredAlgorithms" 含有针对结构化数组的特殊方法的函数的列表 "Summary" 摘要信息,以 Dataset 的方式表示 - Normal[OrthogonalMatrix[…]] 以普通矩阵的形式给出正交矩阵.
- OrthogonalMatrix[…,TargetStructure->struct] 以 struct 指定的格式返回正交矩阵. 可能的设置包括:
-
Automatic 自动选择以何种格式表示矩阵 "Dense" 用稠密矩阵表示 "Structured" 用结构化数组表示 - OrthogonalMatrix[…,TargetStructureAutomatic] 等价于 OrthogonalMatrix[…,TargetStructure"Structured"].
范例
打开所有单元关闭所有单元基本范例 (1)
范围 (5)
OrthogonalMatrix 对象包含提供有关矩阵信息的属性:
应用 (5)
根据 CircularRealMatrixDistribution 构建的矩阵是正交矩阵:
正交矩阵在 ![]() 上保留标准内积. 换句话说,如果
上保留标准内积. 换句话说,如果 ![]() 是正交的且
是正交的且 ![]() 和
和 ![]() 是向量,则
是向量,则 ![]() :
:
任何正交矩阵都表示的是旋转和/或反射. 如果矩阵的行列式为 ![]() ,则为纯旋转. 如果行列式是
,则为纯旋转. 如果行列式是 ![]() ,则矩阵包含反射. 考虑以下矩阵:
,则矩阵包含反射. 考虑以下矩阵:
属性和关系 (1)
OrthogonalMatrix 的转置等价于原矩阵的逆矩阵:
Wolfram Research (2024),OrthogonalMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/OrthogonalMatrix.html.
文本
Wolfram Research (2024),OrthogonalMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/OrthogonalMatrix.html.
CMS
Wolfram 语言. 2024. "OrthogonalMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/OrthogonalMatrix.html.
APA
Wolfram 语言. (2024). OrthogonalMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/OrthogonalMatrix.html 年