ParametricConvexOptimization
ParametricConvexOptimization[f,cons,vars,pars]
パラメータ pars の凸制約 cons に従って凸目的関数 f を最小化する変数 vars の値を求めるParametricFunctionオブジェクトを与える.
ParametricConvexOptimization[…,"prop"]
ParametricFunctionオブジェクトが返すべき解の特性"prop"を指定する.
詳細とオプション




- パラメトリック凸最適化はパラメータに依存する凸制約を使った凸関数の大域的非線形最適化である.与えられたパラメータ値について,大域的最適値が求められる.
- パラメトリック凸最適化は,さまざまなパラメータ値についての最適化を行う際によく使われる.例として,最適値がどのようにパラメータに依存しているかの解析,ベクトル最適化についての最適値のパレート面の計算,確率的最適化のサンプリングメソッド等が挙げられる.
- ParametricConvexOptimizationは結果をParametricFunctionオブジェクトによって与える.
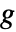 が凹なら,ParametricConvexOptimization[-g,cons,vars,pars]を使って g が最大化できる.
が凹なら,ParametricConvexOptimization[-g,cons,vars,pars]を使って g が最大化できる.- パラメトリック凸最適化は,以下の問題を与えられたパラメータ
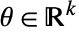 に従って解く
に従って解く 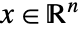 を求める.
を求める. -
最小化 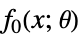
制約条件 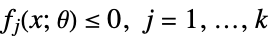
ただし  は凸関数(x 内)
は凸関数(x 内) 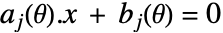 の形の等式制約が cons に含まれることがある.
の形の等式制約が cons に含まれることがある.- 制約条件 cons には,パラメータのみに依存する制約条件
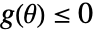 が含まれることがある.これは,返されたParametricFunctionの領域を制約条件が満たされる範囲に制限するために使われる.
が含まれることがある.これは,返されたParametricFunctionの領域を制約条件が満たされる範囲に制限するために使われる. - 結果のParametricFunctionオブジェクトのパラメータについての導関数は,可能な場合は記号と数値の混合感度法を使って計算される.
- 変数およびパラメータの指定の vars および pars は,それぞれ次の形式のいずれかの変数またはパラメータを与える要素のリストでなければならない.
-
v 名前が 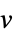 の次元が推定される変数またはスカラーのパラメータ
の次元が推定される変数またはスカラーのパラメータv∈Reals 実スカラー変数 v∈Integers 整数スカラー変数 v∈Complexes 複素スカラー変数 v∈ℛ 幾何学領域 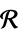 に限定されたベクトル変数
に限定されたベクトル変数v∈Vectors[n,dom] 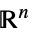 ,
,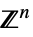 あるいは
あるいは![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/ParametricConvexOptimization.ja/13.png) にあるベクトル変数
にあるベクトル変数v∈Matrices[{m,n},dom]  ,
,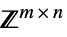 あるいは
あるいは![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/ParametricConvexOptimization.ja/16.png) にある行列変数
にある行列変数 - ParametricConvexOptimizationは,最小化問題を解くのに効率的なメソッドを自動的に見付けるために必要な変換を行う.
- 解かれた主最小化問題には,ラグランジュ双対問題である関連する最大化問題がある.双対最大値は常に主最小値以下であるので,これによって下界が与えられる.双対マキシマイザは,最小値の制約条件における変化に対する感度を含む主問題についての情報を与える.
- 次は,使用可能な解の特性"prop"である.
-
"PrimalMinimizer" 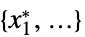
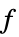 を最小化する変数値のリスト
を最小化する変数値のリスト"PrimalMinimizerRules" 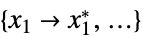
 を最小化する変数 vars={v1,…}の値
を最小化する変数 vars={v1,…}の値"PrimalMinimizerVector" 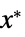
 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 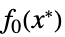
最小値 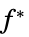
"DualMaximizer" 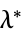
双対問題を最大化するベクトル "DualMaximumValue" 双対最大値 "DualityGap" 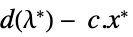
双対最適値と主最適値の差 "Slack" 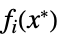
不等式制約を等式制約に変換するベクトル "ConstraintSensitivity" 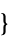
制約摂動に対する 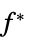 の感度
の感度{"prop1","prop2",…} いくつかの解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する反復の最大数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの面を最適化するか Tolerance Automatic 内部比較で使用する許容範囲 WorkingPrecision MachinePrecision 内部計算に使う精度 - オプションMethodmethod を使って使用するメソッドが指定できる.以下は,使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する solver 可能な場合は,解くために solver を使うように問題を変換する "SCS" SCS(錐ソルバの分割)ライブラリ "CSDP" CSDP(COIN半定値計画)ライブラリ "DSDP" DSDP(半定値計画)ライブラリ - 使用される2つの定式化が solver について文書化された定式化に対応するように,Methodsolver を使って特性のソルバを使うように指定できる.使用可能なソルバには,LinearOptimization,LinearFractionalOptimization,QuadraticOptimization,SecondOrderConeOptimization,SemidefiniteOptimization,ConicOptimization,GeometricOptimizationがある.
- デフォルトで,求まった解はParametricFunctionによってキャッシュされる.
- メモリを節約するためにMethod{method, "ParametricCaching"None}を使って求まった解をキャッシュしないようにすることもできる.
例題
すべて開くすべて閉じるスコープ (32)
基本的な用法 (16)
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表現する:
VectorGreaterEqualを使っていくつかのGreaterEqual不等式制約を一度に表す:
![]() v<=
v<=![]() を使ってベクトル不等式をコンパクトな形式で入力する:
を使ってベクトル不等式をコンパクトな形式で入力する:
Indexedを使ってベクトル変数の成分(![]() )にアクセスする:
)にアクセスする:
定数パラメータ方程式を使って目的関数と制約条件の係数を指定する:
必要なら,Vectors[n,Reals]を使ってベクトル変数の次元を指定する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
Intervalを使って境界を指定する:
Vectors[n,Reals]を使ってベクトルパラメータを指定する:

パラメータについての条件を指定して目的関数および/または制約条件が凸であることを確実にする:
パラメータについての追加的な条件なしでは,凸性は決定できない:
整数変数とパラメータ (6)
Integersを使って整数領域の制約条件を指定する:
Vectors[n,Integers]を使ってベクトル変数についての整数領域の制約条件を指定する:
NonNegativeIntegers (![]() )を使って非負の整数領域制約条件を指定する:
)を使って非負の整数領域制約条件を指定する:
NonPositiveIntegers (![]() )を使って非正の整数領域制約条件を指定する:
)を使って非正の整数領域制約条件を指定する:
Integersを使ってパラメータに対して整数領域を指定する:
Vectors[n,Integers]を使ってベクトル変数パラメータに整数領域を指定する:
複素変数とパラメータ (3)
パラメータ感度 (3)
主モデル特性 (2)
アプリケーション (9)
反復最適化 (1)
幾何問題 (2)
データフィッティング問題 (2)
サンプル誤差 ![]() が正規分布に従っている場合の線形近似係数の近似分布を求める:
が正規分布に従っている場合の線形近似係数の近似分布を求める:
ParametricFunctionは,特定の誤差の例に対してフィット係数![]() を与える:
を与える:
各例を正則化せずにフィット係数を計算し,係数の分布を求める:
ポートフォリオ最適化 (1)
リスクを最小限に抑えながらリターンを最大化するために6つの株式に投資するための資本 ![]() の分布を求める:
の分布を求める:
リターンは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は個々の株式の期待リターン値のベクトルである:
は個々の株式の期待リターン値のベクトルである:
目的は,指定されたリスク回避パラメータ ![]() についてのリスクを最小にしてリターンを最大にすることである:
についてのリスクを最小にしてリターンを最大にすることである:
株式の売買による株式の市場価格への影響は,![]() でモデル化される.これは,エピグラフ変換を使ったPower Coneによってモデル化できる:
でモデル化される.これは,エピグラフ変換を使ったPower Coneによってモデル化できる:
重み ![]() はどれも0より大きく重みと市場への影響のコストの合計は1でなければならない:
はどれも0より大きく重みと市場への影響のコストの合計は1でなければならない:
リスク回避パラメータの範囲について,リターンと対応するリスクを計算する:
範囲 ![]() における最適な
における最適な ![]() はリターンとリスクの間のトレードオフの上限包絡線である:
はリターンとリスクの間のトレードオフの上限包絡線である:
市場コストを考慮することで,低リスク回避のため分散ポートフォリオが得られるが,リスク回避が高い場合,分散の少ない株式を購入するために市場の影響コストが支配的になる:
軌道最適化問題 (2)
![]() に従って
に従って ![]() を最小化する.最小化関数積分は台形規則を使って近似できる.離散化された目的関数は
を最小化する.最小化関数積分は台形規則を使って近似できる.離散化された目的関数は ![]() になる:
になる:
制約条件 ![]() はIndexed関数を使って表すことができる:
はIndexed関数を使って表すことができる:
制約条件 ![]() は有限差分を使って離散化できる.最初と最後の行だけが使われる:
は有限差分を使って離散化できる.最初と最後の行だけが使われる:
障害物を避けながら2点間の最短距離を求める.障害物を指定する:
辺における潜在的な交差を避けるために領域を膨らませることができるが,結果はもとの領域について有効である:
初期点はパラメータ ![]() によって与えられる.最終点は固定されている:
によって与えられる.最終点は固定されている:
経路は ![]() 個の点を使って離散化できる.
個の点を使って離散化できる.![]() が位置ベクトルを表すとする:
が位置ベクトルを表すとする:
![]() の要素の少なくとも1つが0より小さければ点
の要素の少なくとも1つが0より小さければ点 ![]() はオブジェクトの外にある.この制約条件を矯正するために,
はオブジェクトの外にある.この制約条件を矯正するために,![]() が決定ベクトルで
が決定ベクトルで ![]() が
が![]() となるような
となるような ![]() の
の ![]()
![]() 番目の要素であるとすると
番目の要素であるとすると ![]() と
と ![]() は
は ![]() となるために十分大きい:
となるために十分大きい:
テキスト
Wolfram Research (2020), ParametricConvexOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
CMS
Wolfram Language. 2020. "ParametricConvexOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
APA
Wolfram Language. (2020). ParametricConvexOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html
