ParametricConvexOptimization[f,cons,vars,pars]
gives a ParametricFunction object that finds values of variables vars that minimize the convex objective function f subject to convex constraints cons with parameters pars.
ParametricConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned by the ParametricFunction object.


ParametricConvexOptimization
ParametricConvexOptimization[f,cons,vars,pars]
gives a ParametricFunction object that finds values of variables vars that minimize the convex objective function f subject to convex constraints cons with parameters pars.
ParametricConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned by the ParametricFunction object.
Details and Options





- Parametric convex optimization is a global nonlinear optimization for convex functions with convex constraints both depending on parameters. For given parameter values, a global optimum is found.
- Parametric convex optimization is typically used when doing optimization for many different parameter values. Examples include analyzing how the optimum depends on parameters, computing Pareto surfaces of optimal values for vector optimization and sampling methods for stochastic optimization.
- ParametricConvexOptimization gives results in terms of ParametricFunction objects.
- If
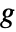 is concave, ParametricConvexOptimization[-g,cons,vars,pars] can be used to maximize g.
is concave, ParametricConvexOptimization[-g,cons,vars,pars] can be used to maximize g. - Parametric convex optimization finds
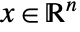 that solves the following problems for given parameters
that solves the following problems for given parameters 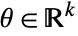 :
: -
minimize 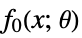
subject to constraints 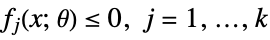
where 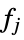 are convex functions in x
are convex functions in x - Equality constraints of the form
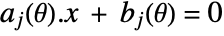 may be included in cons.
may be included in cons. - The constraints cons may include constraints
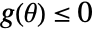 that only depend on parameters. These will be used to restrict the domain of the returned ParametricFunction to where those constraints are satisfied.
that only depend on parameters. These will be used to restrict the domain of the returned ParametricFunction to where those constraints are satisfied. - Derivatives of the resulting ParametricFunction object with respect to the parameters are computed using a combination of symbolic and numerical sensitivity methods when possible.
- The variable and parameters specifications vars and pars should each be a list with elements giving variables or parameters in one of the following forms:
-
v variable with inferred dimensions or scalar parameter with name 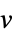
v∈Reals real scalar variable v∈Integers integer scalar variable v∈Complexes complex scalar variable v∈ℛ vector variable restricted to the geometric region 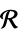
v∈Vectors[n,dom] vector variable in 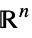 ,
, 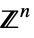 or
or ![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/ParametricConvexOptimization.en/13.png)
v∈Matrices[{m,n},dom] matrix variable in 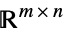 ,
, 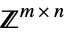 or
or ![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/ParametricConvexOptimization.en/16.png)
- ParametricConvexOptimization automatically does transformations necessary to find an efficient method to solve the minimization problem.
- The primal minimization problem as solved has a related maximization problem that is the Lagrangian dual problem. The dual maximum value is always less than or equal to the primal minimum value, so it provides a lower bound. The dual maximizer provides information about the primal problem, including sensitivity of the minimum value to changes in the constraints.
- The possible solution properties "prop" include:
-
"PrimalMinimizer" 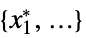
a list of variable values that minimize 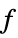
"PrimalMinimizerRules" 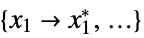
values for the variables vars={v1,…} that minimize 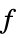
"PrimalMinimizerVector" 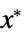
the vector that minimizes 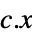
"PrimalMinimumValue" 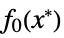
the minimum value 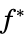
"DualMaximizer" 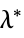
the vectors that maximize the dual problem "DualMaximumValue" the dual maximum value "DualityGap" 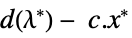
the difference between the dual and primal optimal values "Slack" 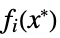
vectors that convert inequality constraints to equality "ConstraintSensitivity" 
sensitivity of 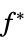 to constraint perturbations
to constraint perturbations{"prop1","prop2",…} several solution properties - The following options may be given:
-
MaxIterations Automatic maximum number of iterations to use Method Automatic the method to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons WorkingPrecision MachinePrecision precision to use in internal computations - The option Methodmethod may be used to specify the method to use. Available methods include:
-
Automatic choose the method automatically solver transform the problem, if possible, to use solver to solve the problem "SCS" SCS (splitting conic solver) library "CSDP" CSDP (COIN semidefinite programming) library "DSDP" DSDP (semidefinite programming) library - Methodsolver may be used to specify that a particular solver be used so that the dual formulation used corresponds to the formulation documented for solver. Possible solvers are LinearOptimization, LinearFractionalOptimization, QuadraticOptimization, SecondOrderConeOptimization, SemidefiniteOptimization, ConicOptimization and GeometricOptimization.
- By default, solutions found are cached by the ParametricFunction.
- Method{method,"ParametricCaching"None} may be used to prevent caching solutions found to save memory.
Examples
open all close allBasic Examples (2)
Scope (32)
Basic Uses (16)
Minimize ![]() subject to
subject to ![]() with parameter
with parameter ![]() :
:
Minimize ![]() subject to
subject to ![]() and parameter
and parameter ![]() :
:
Minimize ![]() subject to
subject to ![]() and parameters
and parameters ![]() :
:
Use VectorLessEqual to express several LessEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use VectorGreaterEqual to express several GreaterEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
Specify the constraints using a combination of scalar and vector inequalities:
An equivalent form using scalar inequalities:
Use vector variables and vector inequalities to specify the problem:
Minimize the function ![]() subject to the constraint
subject to the constraint ![]() and parameters
and parameters ![]() :
:
Use Indexed to access components of a vector variable, e.g. ![]() :
:
Use constant parameter equations to specify the coefficients of the objective and constraints:
Minimize the function ![]() subject to
subject to ![]() and parameter
and parameter ![]() :
:
Use Vectors[n,Reals] to specify the dimensions of vector variables when needed:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequalities:
Specify non-positive constraints using NonPositiveReals (![]() ):
):
Specify bounds using Interval:
Use Vectors[n,Reals] to specify vector parameters:
Specify constraints on the parameter to ensure feasibility:
The constraint cannot be satisfied with ![]() :
:
Specify constraints on the parameter to ensure that the objective and/or constraints are convex:
Without the additional constraint on the parameter, the convexity cannot be determined:
Integer Variables and Parameters (6)
Specify integer domain constraints using Integers:
Visualize the dependence of parameter on the minimum value:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Specify integer domain on parameters using Integers:
A message is issued if noninteger values are given for the parameters:
Specify integer domain on vector variable parameters using Vectors[n,Integers]:
Complex Variables and Parameters (3)
Specify complex variables and parameters using Complexes:
Minimize a real objective ![]() with complex variables and complex constraints
with complex variables and complex constraints ![]() :
:
Let ![]() . Expanding out the constraints into real components gives:
. Expanding out the constraints into real components gives:
Specify a real-valued objective with a vector parameter ![]() :
:
Specify complex ![]() -dimensional vector variables and parameters using Vectors[n,Complexes]:
-dimensional vector variables and parameters using Vectors[n,Complexes]:
Parametric Sensitivity (3)
Plot the derivative of the minimum value with respect to a parameter:
Find the sensitivity of least-squares fit coefficients to a data outlier:
Define a function to give the fit coefficients' residual, slope and intercept {r,m,b} as a function of the measured values ![]() :
:
Show the data with the least-squares fit:
Define a function that gives the derivative with respect to the first measured value and compute it for the data values:
Define a function that gives the derivative with respect to the fifth measured value and compute it for the data values:
The fit is much less sensitive to the fifth than the first value.
Show how a minimizer changes with the direction of the objective vector ![]() :
:
Define a function to get the Jacobian matrix of the minimizer with respect to ![]() :
:
Consider a parametrization of the direction ![]() . The derivative with respect to
. The derivative with respect to ![]() is given by
is given by ![]() :
:
Show the minimizer and its derivative vector with respect to ![]() with the convex region defined by the constraints for a few values of
with the convex region defined by the constraints for a few values of ![]() :
:
Primal Model Properties (2)
Minimize Cos(3α)x+Sin(2α)y over a disk ![]() for varying parameter
for varying parameter ![]() :
:
Get the primal minimizer as a rule:
Get the primal minimizer as a vector:
Show how the position of the minimizer changes with ![]() :
:
Plot the minimal value as a function of ![]() :
:
Use the epigraph transformation to get the primal minimum value as part of the primal minimizer:
The slack for an inequality ![]() at the minimizer
at the minimizer ![]() is given by
is given by ![]() :
:
Dual Model Properties (2)
Minimize ![]() subject to
subject to ![]() and
and ![]() and parameters
and parameters ![]() :
:
The dual problem is to maximize ![]() subject to
subject to ![]() :
:
The primal minimum value and the dual maximum value coincide because of strong duality:
That is the same as having a duality gap of zero. In general, ![]() at optimal points:
at optimal points:
Get the dual maximum value and dual maximizer directly using solution properties:
The "DualMaximizer" can be obtained with:
The dual maximizer vector partitions match the number and dimensions of the dual cones:
Applications (9)
Iterated Optimization (1)
Geometric Problems (2)
Maximize the area of a rectangle with perimeter at most 1 and a ratio ![]() of height to width:
of height to width:
The area is given by the negative of the function:
Plot the maximum area as a function of ![]() :
:
The best shape is, not surprisingly, a square. Note the message is because the values of the function are approximated and so have significant variation near the maximum:
Find the minimum distance between two disks of radius 1 centered at ![]() and
and ![]() , where
, where ![]() is a vector parameter. Let
is a vector parameter. Let ![]() be a point on disk 1. Let
be a point on disk 1. Let ![]() be a point on disk 2. The objective is to minimize
be a point on disk 2. The objective is to minimize ![]() subject to constraints
subject to constraints ![]() :
:
Now plot the minimum distance between the two disks for arbitrary parameter values in ![]() :
:
Data-Fitting Problems (2)
Find an approximate distribution for linear fit coefficients when sample error ![]() is normally distributed:
is normally distributed:
The ParametricFunction gives the fit coefficients ![]() for a particular error instance:
for a particular error instance:
Generate 1000 instances of the samples:
Compute fit coefficients with no regularization for each of the instances and find the distribution of the coefficients:
Show the PDF of the distributions, along with a histogram of the data:
Find the Gaussian width parameter ![]() that minimizes the residual for an
that minimizes the residual for an ![]() fit to nonlinear discrete data:
fit to nonlinear discrete data:
Fit the data using the basis ![]() :
:
The function will be approximated by ![]() :
:
Construct a parametric function that gives the residual:
Show the residual as a function of ![]() :
:
Get the fit coefficients corresponding to the minimum residual:
Portfolio Optimization (1)
Find the distribution of capital ![]() to invest in six stocks to maximize return while minimizing risk:
to invest in six stocks to maximize return while minimizing risk:
The return is given by ![]() , where
, where ![]() is a vector of expected return value of each individual stock:
is a vector of expected return value of each individual stock:
The risk is given by ![]() ;
; ![]() is a risk-aversion parameter and
is a risk-aversion parameter and ![]() :
:
The objective is to maximize return while minimizing risk for a specified risk-aversion parameter ![]() :
:
The effect on market prices of stocks due to the buying and selling of stocks is modeled by ![]() , which is modeled by a power cone using the epigraph transformation:
, which is modeled by a power cone using the epigraph transformation:
The weights ![]() must all be greater than 0 and the weights plus market impact costs must add to 1:
must all be greater than 0 and the weights plus market impact costs must add to 1:
Construct a parametric function:
Compute the returns and corresponding risk for a range of risk-aversion parameters:
The optimal ![]() over a range of
over a range of ![]() gives an upper-bound envelope on the tradeoff between return and risk:
gives an upper-bound envelope on the tradeoff between return and risk:
Compute the weights for a specified number of risk-aversion parameters:
By accounting for the market costs, a diversified portfolio can be obtained for low risk aversion, but when the risk aversion is high, the market impact cost dominates due to purchasing a less diversified stock:
Trajectory Optimization Problems (2)
Minimize ![]() subject to
subject to ![]() . The minimizing function integral can be approximated using the trapezoidal rule. The discretized objective function will be
. The minimizing function integral can be approximated using the trapezoidal rule. The discretized objective function will be ![]() :
:
The constraint ![]() can be discretized using finite differences:
can be discretized using finite differences:
The constraints ![]() can be represented using the Indexed function:
can be represented using the Indexed function:
The constraints ![]() can be discretized using finite differences, and only the first and last rows are used:
can be discretized using finite differences, and only the first and last rows are used:
Solve the discretized trajectory problem:
Visualize the result for a range of parameters ![]() :
:
Visualize the second derivative ![]() for a range of parameters
for a range of parameters ![]() :
:
Find the shortest path between two points while avoiding obstacles. Specify the obstacle:
To avoid potential crossings at the edges, the region can be inflated, but the result will be valid for the original region:
Obtain a set of linear inequalities that enclose the inflated obstacle:
The starting point is given by the parameter ![]() , and the ending point is fixed:
, and the ending point is fixed:
The path can be discretized using ![]() points. Let
points. Let ![]() represent the position vector:
represent the position vector:
The objective is to minimize ![]() . Let
. Let ![]() . The objective is transformed to
. The objective is transformed to ![]() :
:
Specify the starting and ending point constraints:
The distance between any two subsequent points should not be too large:
A point ![]() is outside the object if at least one element of
is outside the object if at least one element of ![]() is less than zero. To enforce this constraint, let
is less than zero. To enforce this constraint, let ![]() be a decision vector and
be a decision vector and ![]() be the
be the ![]()
![]() element of
element of ![]() such that
such that ![]() ; then
; then ![]() and
and ![]() is large enough such that
is large enough such that ![]() :
:
Generate a parametric function for solving the optimization problem for different starting points:
Related Guides
History
Text
Wolfram Research (2020), ParametricConvexOptimization, Wolfram Language function, https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
CMS
Wolfram Language. 2020. "ParametricConvexOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
APA
Wolfram Language. (2020). ParametricConvexOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html
BibTeX
@misc{reference.wolfram_2025_parametricconvexoptimization, author="Wolfram Research", title="{ParametricConvexOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_parametricconvexoptimization, organization={Wolfram Research}, title={ParametricConvexOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html}, note=[Accessed: 01-March-2026]}