RobustConvexOptimization[f,ForAll[pars,pcons,vcons],vars]
finds values of vars that give the minimum value of f for vars that satisfy the constraints vcons for all possible values of the parameters pars that satisfy the parametric constraints pcons.
RobustConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned.




RobustConvexOptimization
RobustConvexOptimization[f,ForAll[pars,pcons,vcons],vars]
finds values of vars that give the minimum value of f for vars that satisfy the constraints vcons for all possible values of the parameters pars that satisfy the parametric constraints pcons.
RobustConvexOptimization[…,"prop"]
specifies what solution property "prop" should be returned.
Details and Options





- Robust optimization is also known as worst-case optimization.
- Robust optimization is typically used when solving an optimization problem under uncertainty represented by parameters with parameter constraints.
- Robust optimization gives the most conservative solution in the sense that the optimum given can be achieved for all possible parameter values.
- Robust optimization finds a robust minimizer
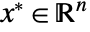 that solves the following problem:
that solves the following problem: -
minimize 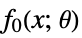
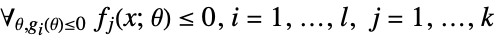
where 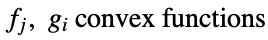
- The robust minimizer
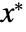 satisfies
satisfies 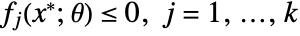 for all
for all 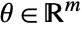 in the parameter set.
in the parameter set. - The robust minimum value
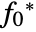 satisfies
satisfies 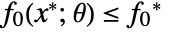 for all
for all 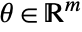 in the parameter set.
in the parameter set. - Linear equality constraints
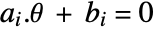 or
or 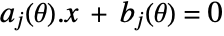 may be included in pcons or vcons.
may be included in pcons or vcons. - RobustConvexOptimization[f,cons,vars,pars] can also be used. The constraints cons are automatically separated into purely parameter constraints
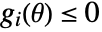 and variable constraints that may depend on parameters
and variable constraints that may depend on parameters 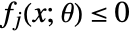 . This form is compatible with ParametricConvexOptimization.
. This form is compatible with ParametricConvexOptimization. - A robust optimization problem is considered tractable if it can be cast into a form where it can be solved or approximated by convex optimization. Tractability depends on a combination of the type of variable constraints
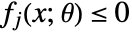 and the type of parameter constraints
and the type of parameter constraints 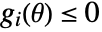 .
. - The following combination of variable constraints and parameter constraints are considered tractable:
-
variable constraints parameter constraints 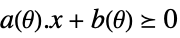
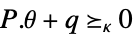
![TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta) TemplateBox[{{{a, ., x}, +, b}}, Norm]<=c(theta).x+d(theta)](Files/RobustConvexOptimization.en/19.png)
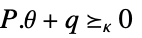
![TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d TemplateBox[{{{{a, (, theta, )}, ., x}, +, {b, (, theta, )}}}, Norm]<=c.x+d](Files/RobustConvexOptimization.en/21.png)
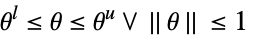
![TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r) TemplateBox[{{{{a, (, {theta, _, l}, )}, ., x}, +, {b, (, {theta, _, l}, )}}}, Norm]<=c(theta_r).x+d(theta_r)](Files/RobustConvexOptimization.en/23.png)
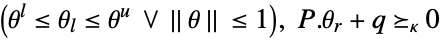
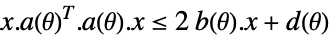
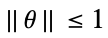
![a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0 a_0(theta)+a_1(theta) x_1+...+a_k(theta) x_k>=_(TemplateBox[{n}, SemidefiniteConeList])0](Files/RobustConvexOptimization.en/27.png)
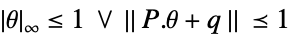
- In general, the variable constraints
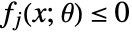 are transformed into conic constraints of the form
are transformed into conic constraints of the form 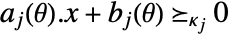 , where
, where 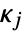 is one of "NonNegativeCone" , "NormCone" or "SemidefiniteCone", and the dependence of
is one of "NonNegativeCone" , "NormCone" or "SemidefiniteCone", and the dependence of 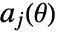 and
and 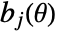 on the parameters should be affine.
on the parameters should be affine. - When the objective function
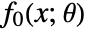 depends on parameters or is nonlinear, an additional variable
depends on parameters or is nonlinear, an additional variable 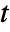 is introduced and the problem is transformed with the epigraph transformation to have objective
is introduced and the problem is transformed with the epigraph transformation to have objective 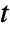 with an additional constraint
with an additional constraint 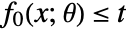 .
. - The variable and parameters specifications vars and pars should each be a list with elements giving variables or parameters in one of the following forms:
-
v variable with inferred dimensions or scalar parameter with name 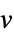
v∈Reals real scalar variable v∈Integers integer scalar variable v∈Complexes complex scalar variable v∈ℛ vector variable restricted to the geometric region 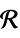
v∈Vectors[n,dom] vector variable in 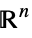 ,
, 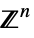 or
or ![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/RobustConvexOptimization.en/42.png)
v∈Matrices[{m,n},dom] matrix variable in 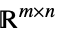 ,
, 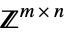 or
or ![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/RobustConvexOptimization.en/45.png)
- The possible solution properties "prop" include:
-
"PrimalMinimizer" 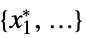
a list of variable values that minimizes 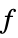
"PrimalMinimizerRules" 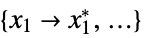
values for the variables vars={v1,…} that minimize 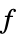
"PrimalMinimizerVector" 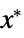
the vector that minimizes 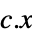
"PrimalMinimumValue" 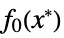
the minimum value 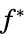
{"prop1","prop2",…} several solution properties - The following options may be given:
-
MaxIterations Automatic maximum number of iterations to use Method Automatic the method to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize Tolerance Automatic the tolerance to use for internal comparisons - The option Methodmethod may be used to specify the method to use. Available methods include:
-
Automatic choose the method automatically "CuttingSet" use a cutting set method "PolyhedralApproximation" approximate "NormCone" constraints with a set of linear constraints "SCS" SCS (splitting conic solver) library "CSDP" CSDP (COIN semidefinite programming) library "DSDP" DSDP (semidefinite programming) library - Some robust optimization problems that are not tractable can be approximately be solved using cutting set methods.
Examples
open all close allBasic Examples (2)
Scope (29)
Basic Uses (15)
Find a robust minimizer for ![]() subject to
subject to ![]() for all
for all ![]() such that
such that ![]() :
:
Find a robust minimizer for ![]() subject to
subject to ![]() for all
for all ![]() in the interval
in the interval ![]() :
:
Find a robust minimizer for ![]() subject to
subject to ![]() for all
for all ![]() such that
such that ![]() :
:
Find a robust minimizer for ![]() subject to
subject to ![]() for all
for all ![]() such that
such that ![]() :
:
Use alternate syntax without an explicit ForAll:
This syntax can be used directly in ParametricConvexOptimization to try particular values of ![]() :
:
Use VectorLessEqual to express several LessEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use VectorGreaterEqual to express several GreaterEqual inequality constraints at once:
Use ![]() v>=
v>=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
Specify the constraints using a combination of scalar and vector inequalities:
An equivalent form using scalar inequalities:
Use vector variables and vector inequalities to specify the problem:
Minimize the function ![]() subject to the constraint
subject to the constraint ![]() for all
for all ![]() such that
such that ![]() :
:
Use Indexed to access components of a vector variable, e.g. ![]() :
:
Use constant parameter equations to specify the coefficients of the objective and constraints:
Minimize the function ![]() subject to
subject to ![]() for all
for all ![]() such that
such that ![]() :
:
Use Vectors[n,Reals] to specify the dimension of vector variables when needed:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequalities:
Specify non-positive constraints using NonPositiveReals (![]() ):
):
Specify bounds using Interval:
Use Evaluate to ensure that the first argument in ForAll gets evaluated when parameters are grouped and assigned to a variable:
Linear Variable Constraints (5)
Find a robust minimizer for ![]() subject to
subject to ![]() for all
for all ![]() in the interval [0,2]:
in the interval [0,2]:
Mathematically the constraint ![]() for all
for all ![]() in [0,2] implies that
in [0,2] implies that ![]() . Thus the problem is equivalent to:
. Thus the problem is equivalent to:
Find a robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that they are constrained to intervals:
such that they are constrained to intervals:
Visualize the minimizer and the variable constraint set for extreme values of ![]() . The set of
. The set of ![]() that is feasible for all possible values of the parameters
that is feasible for all possible values of the parameters ![]() , shown in green, is the intersection of the parametric feasible regions:
, shown in green, is the intersection of the parametric feasible regions:
Find a robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that they are constrained to intervals:
such that they are constrained to intervals:
Visualize the minimizer, the variable constraint set for extreme values of the parameter ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of the parameter ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
For extreme parameter values ![]() , find the range for
, find the range for ![]() for which the matrix
for which the matrix ![]() is positive semidefinite:
is positive semidefinite:
Visualize the minimizer and the feasible region (shown in green) formed by intersection of regions produced by varying ![]() :
:
NormCone Variable Constraints (7)
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer and the variable constraint set for extreme values of ![]() . The set of
. The set of ![]() that is feasible for all possible values of the parameters
that is feasible for all possible values of the parameters ![]() is the intersection of all feasible regions (shown in green):
is the intersection of all feasible regions (shown in green):
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of the parameter ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find a robust minimizer for ![]() over variable constraints
over variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
SemidefiniteCone Variable Constraints (2)
Find an approximate robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of the parameter ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Find an approximate robust minimizer for ![]() subject to variable constraints
subject to variable constraints ![]() for all
for all ![]() such that
such that ![]() :
:
Visualize the minimizer, the variable constraint set for extreme values of the parameter ![]() and the feasible region (shown in green):
and the feasible region (shown in green):
Options (3)
Method (2)
Use Method"CuttingSet" to solve problems whose robust counterparts are not tractable:

Visualize the minimizer and the variable constraint set for two extreme values of the parameter along with the feasible region (shown in green):
Use Method"PolyhedralApproximation" to linearize "NormCone" constraints. This enables approximate solution problems with otherwise intractable robust counterparts:

Visualize the minimizer and the variable constraint set for two extreme values of the parameter:
Applications (14)
Geometry Problems (2)
Find the center ![]() and radius
and radius ![]() of the smallest circle that encloses a set of subcircles:
of the smallest circle that encloses a set of subcircles:
The subcircles are represented by points that are the centers of uncertainty disks:
The objective is to minimize the radius ![]() subject to the constraints
subject to the constraints ![]() :
:
The center and radius of the disk are:
Find the minimum distance between two disks of radius ![]() and centered at
and centered at ![]() and
and ![]() such that the uncertainties are modeled as an ellipsoid
such that the uncertainties are modeled as an ellipsoid ![]() :
:
Let ![]() and
and ![]() be the points associated with disks 1 and 2. The objective is to minimize the
be the points associated with disks 1 and 2. The objective is to minimize the ![]() subject to
subject to ![]() :
:
The minimum distance between the two disks with center and radius uncertainties is:
Visualize the positions of the two points, along with some extreme cases of the uncertainty disks:
Data-Fitting Problems (3)
Find a robust linear fit to data with response subject to interval uncertainty:
The objective is to minimize the error between the input and output subject to the interval uncertainty ![]() :
:
Find slope m and intercept b for a robust fit y=m x+b:
Compare with a simple least-squares fit of the data:
Find fit models for 100 possible realizations of the uncertainty:
Show the envelope of the fit models with the robust fit (black), the simple fit (green) and the data:
Fit a cubic curve to discrete data whose output contains interval uncertainty ![]() :
:
Construct the input matrix using DesignMatrix:
The objective is to minimize the error between the input and output subject to the interval uncertainty ![]() :
:
Find the coefficients associated with each of the bases:
Find fit models for 100 possible realizations of the uncertainty:
Show the envelope of the fit models with the robust fit (black) and the data:
Compare the robust fit (black) and the average model (red) to the exact solution without noise:
The robust fit will tend to have a higher error than the average model:
Fit a cubic curve to discrete data whose instance of measurement (input) is in the uncertain range ![]() :
:
Find the coefficients subject to interval uncertainty ![]() on the input matrix:
on the input matrix:
Show the robust fit with an envelope generated from random instances of the input noise:
Compare the robust fit (black) and the average model (red) to the exact solution without noise:
Manufacturing Problems (3)
Find the optimal mix of two drugs ![]() for a company to manufacture to maximize profit given uncertainty in extracting the active agents from two different raw materials
for a company to manufacture to maximize profit given uncertainty in extracting the active agents from two different raw materials ![]() . The revenue per unit of drugs is:
. The revenue per unit of drugs is:
The company can only store 1000 kg of raw materials:
It requires 90 to 100 hours of manpower to manufacture the two drugs. The company has only 2000 hours of manpower available:
It requires 40 to 50 hours of equipment time to manufacture the two drugs. The company has only 800 hours of equipment time available:
The operational costs for manufacturing the two drugs are 700 and 800, respectively. The raw material costs per kilogram are 100 and 199.9, respectively:
The company has a total budget of $100,000:
The company must manufacture some units of drugs, and therefore must buy some raw materials:
The amounts of active agent extracted from the two raw materials are ![]() g/kg and
g/kg and ![]() g/kg of raw materials, respectively. The two drugs need 0.5 g/unit and 0.6 g/unit of active agent, respectively:
g/kg of raw materials, respectively. The two drugs need 0.5 g/unit and 0.6 g/unit of active agent, respectively:
The objective is to maximize revenue while minimizing purchasing and operational costs:
The profit, taking the uncertainties into account, is:
Construct a parametric function for the problem:
Without the active agent fluctuations in the raw materials, the second raw material is preferred:
The profit without the uncertainties is:
Taking uncertainties into account, there will be at most a 6% reduction in profit:
The robust solution corresponds to the worst-case scenario of the least amount of active agent being extracted from the raw materials:
To see the advantage of using the robust solution, generate a parametric function with the raw materials and the active agent uncertainty as parameters:
If the raw materials are purchased using the nominal result, i.e. ![]() , then the profit may decrease by 21% depending on the amount of active agent that can be extracted from the raw material:
, then the profit may decrease by 21% depending on the amount of active agent that can be extracted from the raw material:
If the raw materials are purchased using robust result, i.e. ![]() , then the profit may decrease by at most 6%:
, then the profit may decrease by at most 6%:
Plot the profit as a function of the active agent that can be extracted from the second raw material:
Find the mix of products to manufacture that maximizes the profits of a company where there is some uncertainty in the manufacturing inputs. The company makes three products. Under ideal conditions, the revenue per unit, cost per unit and maximum capacity are given by:
Each product is made using four machines. The time a machine spends on each product is:
Due to market fluctuations, the revenue generated by each unit of product may decrease by $5:
Accounting for machine downtime, the manufacturing capacity may decrease by 5 units per product:
Each machine can run at most 2400 minutes per week. If a machine is not operational, then it takes at most 120 minutes to return it to working condition:
The cost for repairing any of the four machines increases the cost of each product by $5 per unit:
The profit equals revenue minus cost times the number of units ![]() for product
for product ![]() :
:
Gather all the variable constraints:
Gather all the parameter constraints:
Gather all the parameter specifications:
The objective is to maximize the profit. The optimal product mix is given by:
Construct a parametric function for varying the various parameters:
The best-case scenario would involve no revenue decrease or machine downtime and is given by:
The worst-case scenario corresponds to the result obtained by RobustConvexOptimization:
Find the mix of products to manufacture that maximizes the profits of a company that sells three products ![]() subject to price and supply fluctuation:
subject to price and supply fluctuation:
The revenue per unit accounting for price fluctuation of ![]() per unit is:
per unit is:
The factory is only open for 100 days. Ideally, it takes 2, 4 or 5 days to make each unit but, due to unexpected delays, the manufacturing time might increase by a day:
Each product contains gold and tin. The total gold and tin available are ![]() and
and ![]() units, respectively:
units, respectively:
The company incurs a setup cost for each product if that product is manufactured:
Because of the relatively high setup costs, it may be desirable not to manufacture some of the products at all. Let ![]() be a decision variable such that
be a decision variable such that ![]() if product
if product ![]() is manufactured, and otherwise
is manufactured, and otherwise ![]() . The limit
. The limit ![]() ensures that if
ensures that if ![]() is 0, so is
is 0, so is ![]() , without limiting the size of
, without limiting the size of ![]() more than other constraints do:
more than other constraints do:
The objective is to maximize the profit:
Collect all the variable constraints:
Collect the parameter constraints:
Collect the parameter specifications:
Construct a parametric function for varying the various parameters:
The result matches the worst-case scenario, which is given by:
Structural Optimization Problems (1)
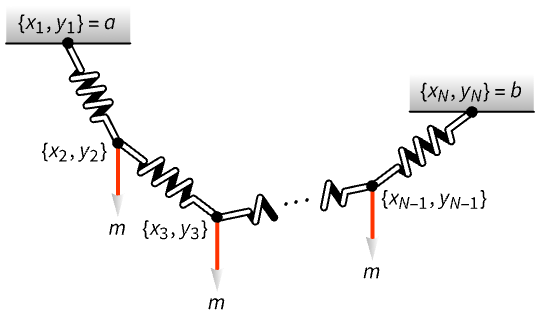
Find the shape of a hanging chain formed by ![]() spring links under a vertical load at the end of each link where both the stiffness and equilibrium lengths of the springs are subject to manufacturing uncertainty. The objective is to find the link positions
spring links under a vertical load at the end of each link where both the stiffness and equilibrium lengths of the springs are subject to manufacturing uncertainty. The objective is to find the link positions ![]() :
:
The potential energy due to gravity is ![]() , where
, where ![]() is the vertical load at each end and
is the vertical load at each end and ![]() is gravity:
is gravity:
The potential energy due to the tension in the spring link due to stretching is ![]() , where
, where ![]() is the stretch in spring link
is the stretch in spring link ![]() ,
, ![]() is the uncertain stiffness of the spring and
is the uncertain stiffness of the spring and ![]() is the ideal stiffness of the spring. Using
is the ideal stiffness of the spring. Using ![]() , the energy is transformed to
, the energy is transformed to ![]() :
:
An additional constraint ![]() must be added due to the transformation:
must be added due to the transformation:
The ends of the linked chain are clamped at positions (0,0) and (2,-1):
Each link has to satisfy the condition ![]() , where
, where ![]() is the resting length of each spring subject to uncertainty
is the resting length of each spring subject to uncertainty ![]() :
:
The design constant parameters are:
The final objective function is the sum of gravity and spring potential energy that must be minimized:
Find the end points of each of the spring links:
Visualize the shape of the resulting spring chain:
The stretch is greatest for the links near the ends of the link chain. Link 12 has the least elongation:
Portfolio Optimization (2)
Find the best combination of six stocks to invest in out of a possible 20 candidate stocks subject to market volatility, so as to maximize return while minimizing risk when there is uncertainty in the mean returns. The expected return values ![]() for stock
for stock ![]() and the covariance between the stocks
and the covariance between the stocks ![]() are:
are:
Due to market fluctuations, the average return value of each stock is subject to an uncertainty ![]() :
:
Let ![]() be the percentage of total investment made in stock
be the percentage of total investment made in stock ![]() . The return is given by
. The return is given by ![]() :
:
Let ![]() be a decision vector such that if
be a decision vector such that if ![]() , then that stock is bought. Six stocks have to be chosen:
, then that stock is bought. Six stocks have to be chosen:
The percentage of investment ![]() must be greater than 0 and must add to 1:
must be greater than 0 and must add to 1:
Find the optimal combination of stocks that minimizes the risk and maximizes return:
The safest optimal combination of stocks is:
The percentages of investment to put into the respective stocks are:
The safe risks and returns are:
Construct a parametric function for varying the various parameters:
The safest optimal stock combination gives the smallest risk and return compared to optimal stocks with random instances of uncertainties:
Find the distribution of capital to invest in six stocks to maximize return while minimizing risk when there is uncertainty in both the mean returns and covariance. The expected return values ![]() for stock
for stock ![]() and the covariance between the stocks
and the covariance between the stocks ![]() are:
are:
Due to market fluctuations, the return value of each stock is subject to an uncertainty ![]() :
:
Let ![]() be the percentage of total investment made in stock
be the percentage of total investment made in stock ![]() . The return is given by
. The return is given by ![]() :
:
The covariance is extracted from a finite dataset and is also subject to uncertainties ![]() :
:
The risk is given by ![]() , and
, and ![]() is a risk-aversion parameter:
is a risk-aversion parameter:
The objective is to maximize return while minimizing risk for a specified risk-aversion parameter ![]() :
:
The percentage of investment ![]() must be greater than 0 and must add to 1:
must be greater than 0 and must add to 1:
Compute the returns and corresponding risk for a range of risk-aversion parameters:
Increasing the risk-aversion parameter ![]() leads to stock diversification to reduce the risk:
leads to stock diversification to reduce the risk:
Facility Location Problems (1)
A company wants to open a new factory. The factory needs raw materials from five warehouses. The transportation cost per unit distance, which varies between ![]() , between the new factory and warehouses is:
, between the new factory and warehouses is:
Let ![]() be the distance between factory and warehouses
be the distance between factory and warehouses ![]() The objective is to minimize
The objective is to minimize ![]() :
:
The five warehouses ![]() are located at:
are located at:
The new factory ![]() must be located such that
must be located such that ![]() :
:
Find the optimal distances between the new factory and the warehouses:
The new factory location is closer to the warehouses, where the transportation costs are higher:
Classification Problems (2)
Find a line ![]() that separates two groups of points
that separates two groups of points ![]() and
and ![]() where
where ![]() are interval uncertainties:
are interval uncertainties:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
The objective is to minimize ![]() , which gives twice the thickness between
, which gives twice the thickness between ![]() and
and ![]() :
:
Visualize the classifier subject along with the box uncertainty for each point:
Increasing the box uncertainty will lead to an infeasible classifier:
Visualizing the sets with the increased uncertainties shows that the two sets have some points whose uncertainty boxes overlap:
Find a quadratic polynomial that separates two groups of 3D points ![]() and
and ![]() where
where ![]() are interval uncertainties:
are interval uncertainties:
Construct the quadratic polynomial data matrices for the two sets using DesignMatrix:
For separation, set 1 must satisfy ![]() and set 2 must satisfy
and set 2 must satisfy ![]() :
:
Find the separating polynomial by minimizing ![]() :
:
Related Guides
History
Text
Wolfram Research (2020), RobustConvexOptimization, Wolfram Language function, https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
CMS
Wolfram Language. 2020. "RobustConvexOptimization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RobustConvexOptimization.html.
APA
Wolfram Language. (2020). RobustConvexOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RobustConvexOptimization.html
BibTeX
@misc{reference.wolfram_2025_robustconvexoptimization, author="Wolfram Research", title="{RobustConvexOptimization}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/RobustConvexOptimization.html}", note=[Accessed: 06-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_robustconvexoptimization, organization={Wolfram Research}, title={RobustConvexOptimization}, year={2020}, url={https://reference.wolfram.com/language/ref/RobustConvexOptimization.html}, note=[Accessed: 06-March-2026]}