ParametricConvexOptimization
ParametricConvexOptimization[f,cons,vars,pars]
给出一个 ParametricFunction 对象,它能求出可最小化受含有参数 pars 的凸约束条件 cons 限制的凸目标函数 f 的变量 vars 的值.
ParametricConvexOptimization[…,"prop"]
指定 ParametricFunction 对象应返回的解的属性 "prop".
更多信息和选项



- 参数化条件下的凸优化是针对凸函数的全局非线性优化,凸函数和凸约束条件均依赖于参数. 对于给定的参数值,求全局最优值.
- 对许多不同的参数值进行优化时,通常会使用参数化条件下的凸优化. 给出的范例包括分析最佳值如何取决于参数,计算向量优化的最佳值的帕累托曲面以及用于随机优化的采样方法.
- ParametricConvexOptimization 用 ParametricFunction 对象的形式给出结果.
- 如果
 是凹的,ParametricConvexOptimization[-g,cons,vars,pars] 可用于最大化 g.
是凹的,ParametricConvexOptimization[-g,cons,vars,pars] 可用于最大化 g. - 对于给定参数
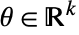 ,参数化条件下的凸优化给出可求解以下问题的
,参数化条件下的凸优化给出可求解以下问题的 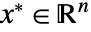 :
: -
最小化 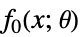
受以下约束条件限制 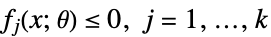
其中 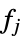 是 x 的凸函数
是 x 的凸函数 - 可将形为
 的等式约束条件包括在 cons 中.
的等式约束条件包括在 cons 中. - 约束条件 cons 只可包含取决于参数的约束条件
 . 这些条件被用于将返回的 ParametricFunction 的定义域限制为满足这些约束条件的区域.
. 这些条件被用于将返回的 ParametricFunction 的定义域限制为满足这些约束条件的区域. - 在可能的情况下,使用符号敏感度和数字敏感度方法的组合来计算所得 ParametricFunction 对象关于参数的导数.
- 变量和参数指定 vars 和 pars 都应该是列表,其中的元素应给出以下形式的变量或参数:
-
v 名为 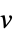 的维度由推断而得的变量或标量参数
的维度由推断而得的变量或标量参数v∈Reals 实标量变量 v∈Integers 整数标量变量 v∈Complexes 复标量变量 v∈ℛ 限制于几何区域  的向量变量
的向量变量v∈Vectors[n,dom] 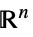 、
、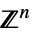 或
或 ![TemplateBox[{}, Complexes]^n TemplateBox[{}, Complexes]^n](Files/ParametricConvexOptimization.zh/13.png) 中的向量变量
中的向量变量v∈Matrices[{m,n},dom]  、
、 或
或 ![TemplateBox[{}, Complexes]^(m x n) TemplateBox[{}, Complexes]^(m x n)](Files/ParametricConvexOptimization.zh/16.png) 中的矩阵变量
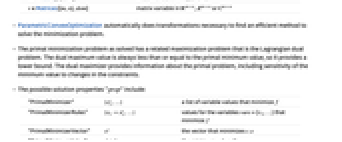
中的矩阵变量 - ParametricConvexOptimization 自动进行必要的转换,以找到求解最小化问题的高效方法.
- 原始最小化问题有相关的最大化问题,即拉格朗日对偶问题. 对偶最大值始终小于或等于原始最小值,因此它给出了下限. 对偶最大值点提供了有关原始问题的信息,包括最小值对约束条件变化的敏感性.
- 可能的解的属性 "prop" 包括:
-
"PrimalMinimizer" 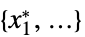
最小化 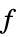 的变量值列表
的变量值列表"PrimalMinimizerRules" 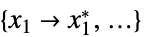
最小化 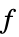 的变量 vars={v1,…} 的值
的变量 vars={v1,…} 的值"PrimalMinimizerVector" 
最小化 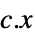 的向量
的向量"PrimalMinimumValue" 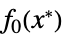
最小值 
"DualMaximizer" 
最大化对偶问题的向量 "DualMaximumValue" 对偶最大值 "DualityGap" 
对偶值和原始最优值之间的差 "Slack" 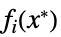
将不等式约束条件转化为等式约束条件的向量 "ConstraintSensitivity" 
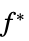 对约束条件扰动的敏感性
对约束条件扰动的敏感性{"prop1","prop2",…} 解的几个属性 - 可给出以下选项:
-
MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PerformanceGoal $PerformanceGoal 优化的目标 Tolerance Automatic 内部比较采用的容差 WorkingPrecision MachinePrecision 内部计算使用的精度 - 选项 Methodmethod 可用来指定使用的方法. 可用的方法包括:
-
Automatic 自动选择方法 solver 可能的情况下,对问题进行转化,以便使用 solver 求解问题 "SCS" SCS (splitting conic solver) 库 "CSDP" CSDP (COIN semidefinite programming) 库 "DSDP" DSDP (semidefinite programming) 库 - Methodsolver 可以用来指定使用特定的求解器,以便所用的对偶问题对应于适合于用 solver 求解的问题. 可能的求解器有 LinearOptimization、LinearFractionalOptimization、QuadraticOptimization、SecondOrderConeOptimization、SemidefiniteOptimization、ConicOptimization 和 GeometricOptimization.
- 默认情况下,求得的解由 ParametricFunction 缓存.
- Method{method,"ParametricCaching"None} 可用于防止为节省内存对解进行缓存.
范例
打开所有单元关闭所有单元范围 (32)
基本用法 (16)
用 VectorLessEqual 一次性表示几个 LessEqual 不等式约束条件:
用 VectorGreaterEqual 同时表示几个 GreaterEqual 不等式约束条件:
用 Indexed 指定向量变量的分量,如 ![]() :
:
必要情况下用 Vectors[n,Reals] 指定向量变量的维度:
用 NonNegativeReals (![]() ) 指定非负约束条件:
) 指定非负约束条件:
用 NonPositiveReals (![]() ) 指定非正约束条件:
) 指定非正约束条件:
用 Interval 指定边界:
整数变量和参数 (6)
用 Integers 指定整数域约束条件:
用 Vectors[n,Integers] 指定向量变量的整数域约束条件:
用 NonNegativeIntegers (![]() ) 指定非负整数域约束条件:
) 指定非负整数域约束条件:
用 NonPositiveIntegers (![]() ) 指定非正整数约束条件:
) 指定非正整数约束条件:
用 Integers 对参数指定整数域约束条件:
用 Vectors[n,Integers] 指定向量变量参数的整数域:
复数变量和参数 (3)
参数化敏感性 (3)
原始模型属性 (2)
应用 (9)
几何问题 (2)
数据拟合问题 (2)
ParametricFunction 给出与特定误差值对应的拟合系数 ![]() :
:
投资组合优化 (1)
轨迹优化问题 (2)
最小化受 ![]() 限制的
限制的 ![]() . 可使用梯形法则近似最小化函数积分. 离散化的目标函数为
. 可使用梯形法则近似最小化函数积分. 离散化的目标函数为 ![]() :
:
可用 Indexed 函数表示约束条件 ![]() :
:
为了避免与障碍物的边相交,可对区域进行放大,但结果将对原始区域有效:
如果 ![]() 中至少有一个元素小于零,则点
中至少有一个元素小于零,则点 ![]() 在障碍物之外. 为了强制实行该约束条件,令
在障碍物之外. 为了强制实行该约束条件,令 ![]() 为决策变量,
为决策变量,![]() 为
为 ![]() 的第
的第 ![]() 个元素,使得
个元素,使得 ![]() ,则
,则 ![]() 和
和 ![]() 足够大,可满足
足够大,可满足 ![]() :
:
文本
Wolfram Research (2020),ParametricConvexOptimization,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
CMS
Wolfram 语言. 2020. "ParametricConvexOptimization." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html.
APA
Wolfram 语言. (2020). ParametricConvexOptimization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ParametricConvexOptimization.html 年