PeriodicBoundaryCondition

PeriodicBoundaryCondition[u[x1,…],pred,f]

表示给予 NDSolve 的区域的边界上、pred 为 True 的所有 xtarget 的周期性边界条件 .

PeriodicBoundaryCondition[a+b u[x1,…],pred,f]

表示广义化的周期性边界条件 .

更多信息

  • PeriodicBoundaryCondition 与微分方程一起使用来描述如 NDSolve 这样的函数中的边界条件.
  • 在 NDSolve[eqns,{u1,u2,…},{x1,x2,…}∈Ω] 中，xi 为独立变量，uj 为因变量， Ω 是边界为 ∂Ω 的区域.
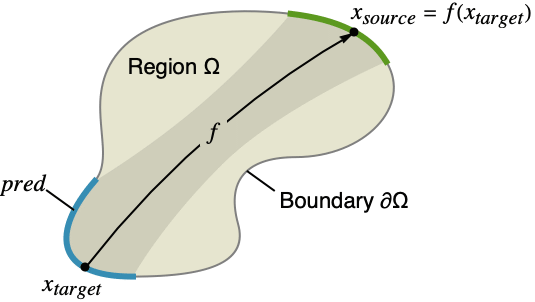
  • 用蓝色显示边界区域被指定的位置. 它们出现在区域 Ω 的边界∂Ω 上，指定了这些位置上的解与绿色所示位置的关系. 函数 f 将解从蓝色位置映射到绿色位置.
  • 在区域 Ω 为矩形的特殊情况下，边界方程 u[…,xi,min,…]u[…,xi,max,…] 被视为等价于 PeriodicBoundaryCondition[u[…,xi,…],xixi,max,f]，同时 f=TranslationTransform[{…,0,xi,min-xi,max,0,…}]. »
  • 独立变量 x1,… 的任何等式与不等式的逻辑组合都可以用于表明 pred.
  • 在 PeriodicBoundaryCondition[a+b u[x1,…],pred,f] 中，对于在 ∂Ω 上 pred 为True 的部分上的任意一个点 xtarget，xsource=f[xtarget] 应为 ∂Ω 中 pred 不为 True 的部分上的一个点.
  • 对于 PeriodicBoundaryCondition[a+b u[x1,…],pred,f]，在 NDSolve 中，系统矩阵被修改以使得解的值 u[xtarget] 近似满足 u[xsource]==a+b u[xtarget]（对于 pred 为 True 的边界 Ω 上的所有 xtarget）.
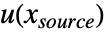  • 的边界条件（包括隐式 Neumann 0 条件）也将映射到 .
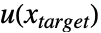  • 在 PeriodicBoundaryCondition[a+b u[x1,…],pred,f] 中，a 和 b 都是标量值，可能依赖于任意一个独立变量 xi，包括时间.
  • 可以用 PeriodicBoundaryCondition[-u[x1,…],pred,f] 指定反周期边界.
  • a 和 b 的常见值包括：
  • u[x1,…]周期性边界条件
    -u[x1,…]反周期性边界条件
    a u[x1,…]缩放过的周期性边界条件
    u[x1,…]+b有偏移的周期性边界条件
  • 对于有限元近似法，在一维情况下，PeriodicBoundaryCondition 在结点上进行操作；二维情况下，在边上进行操作；三维情况下，则在面上进行操作.

范例

打开所有单元关闭所有单元

基本范例  (2)

求周期性边界条件下拉普拉斯方程的 5 个特征值和特征向量：

将所得特征值与解析特征值相比较：

可视化特征函数：

查看边界是否是周期性的：

求解在曲线边界上有周期性边界条件的泊松方程：

可视化解：

可视化周期解：

范围  (15)

1D 特征值问题  (7)

求 Mathieu 方程的 5 个特征值和特征向量：

可视化特征函数：

查看边界是否是周期性的：

和下式等价：

求反周期边界条件下拉普拉斯方程的 5 个特征值和特征向量：

查看特征值：

可视化特征函数：

查看特征向量在端点相加所得的结果：

求 Meissner 方程在精细网格上的 9 个特征值和特征向量：

将特征值与解析特征值比较

可视化特征函数：

求具有对称势的 Sturm–Liouville 算子的 5 个特征值和特征向量：

查看特征值：

用在更高精度重新计算特征值：

可视化特征函数：

求具有不对称势的 Sturm–Liouville 算子的 5 个周期性特征值和特征向量：

查看特征值：

可视化特征函数：

求具有不对称势的 Sturm–Liouville 算子的 5 个反周期特征值和特征向量：

查看特征值：

可视化特征函数：

查看特征向量在端点相加所得的结果：

求具有不对称势的 Sturm–Liouville 算子的 5 个关系反周期特征值和特征向量：

查看特征值：

可视化特征函数：

查看特征向量在端点是否满足相互之间的关系：

1D+ 时间 PDE 问题  (2)

求解周期性边界条件下的 1D Schrödinger 方程：

可视化波函数：

求解周期性边界条件下的 1D 波动方程：

可视化周期性波动方程：

前面的示例使用 作为目标. 在这种情况下，将目标放置在通量进入周期域的位置.

相反，如果 是目标，则波动脉冲在达到 时反转，然后向后移动. 在 时，隐式 Neumann 0 边界条件施加了硬边界条件，脉冲从该硬边界反射出来:

比较两个周期波函数：

2D PDE 问题  (4)

设置矩形区域，求解上面和下面具有 DirichletCondition 的 PDE：

为了实现周期性边界条件，从目标 (x==0) 到源 (x==2) 指定的映射 f：

将周期性边界条件的区域 Ω 和源显示为绿色，将目标显示为蓝色：

用映射函数 f 指定周期性边界条件：

求解并可视化方程：

求在长方形的左下角具有 DirichletCondition、并有周期性边界条件连接至相对位置的拉普拉斯类型方程的解：

可视化结果：

查看边界上解的差别：

注意左下角的 DirichletCondition 已传播至其他的边角：

指定一个区域：

显示区域和边界：

求从目标（蓝色）映射至源（绿色）的映射函数 f：

在内部有热生成和橘色边界上温度恒定的条件下求解泊松方程，同时有周期性边界条件连接绿色源边界和蓝色目标边界：

查看周期性边界是否有相同的值：

可视化解：

与反周期解相比较：

指定一个区域：

下面的部分和上面的部分需满足 DirichletCondition：

左侧的边为右侧的边（源）的相关边界条件的目标：

求解并可视化方程：

查看周期性边界间是否有正确的关系：

2D+ 时间 PDE 问题  (1)

在周期性边界条件下和势能拟合于盒子的情况下求解 2D 含时 Schrödinger 方程：

可视化波动方程：

3D 问题  (1)

在具有周期性边界条件的长方体内求解泊松方程：

可视化解：

应用  (1)

计算 Laplacian 在 Disk 上极坐标的特征值：

解析式计算 Laplacian 在 Disk 上笛卡尔坐标的特征值：

比较计算出的特征值：

数值式计算 Laplacian 在 Disk 上笛卡尔坐标的特征值：

将笛卡尔坐标下计算出的数值计算特征值与解析解进行比较：

比较数值计算的特征值：

可能存在的问题  (8)

仅仅指定静态偏微分方程的周期性边界条件可能导致非惟一解. 有些情况下，可能无法对系统求解：

指定源边界上的 DirichletCondition：

PeriodicBoundaryCondition 的映射函数 f 的源不必在域的边界上：

可视化结果：

注意 :

与源在边界上的解相比较：

可视化结果：

DirichletCondition 不能出现在目标边界上：

把 DirichletCondition 移到源边界上就可以了：

周期性边界条件把 PDE 的解从源传播到目标边界. 把哪个边界作为源，哪个作为目标会影响 PDE 的解.

考虑一个长方形的域和非对称泊松方程：

下面的部分和上面的部分需满足 DirichletCondition：

首先，把左侧的边作为右侧的边（源）的目标边界：

求解并可视化方程：

查看周期性边界上的值：

在第二个例子中，把右侧的边作为左侧的边（源）的目标边界：

求解并可视化方程：

查看周期性边界上的值：

周期性边界条件把 PDE 的解从源区域传播到目标区域. 映射的方向会影响 PDE 的解.

考虑一个长方形的域和非对称泊松方程：

下面的部分和上面的部分需满足 DirichletCondition：

把右下部分映射到左上部分、右上部分映射到左下部分：

左边作为右边的目标边界：

求解并可视化方程：

与映射方向不变但交换边的指定；把右下部分映射到左下部分、右上部分映射到左上部分：

左边作为右边的目标边界：

求解并可视化方程：

周期性边界条件与偏微分方程从源边界到目标边界的求解有关. 源头处存在的边界条件（也包括隐性条件）将影响目标处的解.

这里以一个有限元方法离散的时间相关方程来为例来说明该行为. 指定初始条件 u 和两侧隐式 Neumann 零边界条件，且未指定 PeriodicBoundaryCondition：

在不同时间可视化解：

注意，在两个空间边界处都满足隐式 Neumann 0 边界条件.

在具有隐式 Neumann 0 边界条件的源边界上使用 PeriodicBoundaryCondition 时，该条件将映射到目标边界.

以下是与先前相同的方程和初始条件下的解，附加了一个周期边界条件，其源在左边，目标在右边：

在不同时间可视化解：

注意如何将左侧隐式 Neumann 0 边界条件下的解值映射到右侧.

这是有限元方法的预期行为. 张量积网格方法的行为有所不同，因为该方法没有隐式边界条件：

可视化不同时间的张量积网格解：

通过指定左侧 DirichletCondition 和 PeriodicBoundaryCondition，可以使用有限元方法实现类似的行为：

可视化不同时间的有限元和张量积网格解之间的差：

或者，可以在每一侧指定 DirichletCondition.

周期性边界条件将 PDE 在源处的解与目标边界关联起来. 源处存在的边界条件（包括隐性条件）将影响目标处的解. 可使用多个周期性边界条件来强制有连续的导数.

设置一个区域及一个辅助函数，接受周期性边界条件作为参数：

设置绘图选项及辅助函数以生成周期性绘图：

求解左侧有一个周期性边界条件的 PDE：

显示解的周期性等高线图：

可视化解的梯度的周期性流密度图：

注意，梯度不是连续的. 这是由于在源处出现了隐性 Neumann 值.

同样，可视化解的梯度的范数的周期性密度图：

指定第二个周期性边界条件，强制导数连续. 求解左右两侧都有周期性边界条件的 PDE：

可视化解的周期性等高线图. 不出所料，解已发生改变，因为隐性 Neumann 值已被消除：

可视化解的梯度的周期性流密度图. 注意，梯度现在是连续的：

可视化解的梯度的范数的周期性密度图，梯度的范数也是连续的：

这种方法同样适用于非结构化网格.

周期性边界条件，如 Neumann 值，二维情况下，在边上进行操作；三维情况下，在面上进行操作. 这意味着在有限元网格中需要存在足够多的节点才能使周期性边界条件起作用.

生成有限元网格，并可视化网格的节点：

求解带有映射一个点的周期性边界条件的 PDE：

要解决此问题，为覆盖一条边的周期性边界条件指定一个 predicate：

巧妙范例  (1)

指定一个区域，在一个盒子上求解波动方程：

设置映射函数令有颜色的边相互匹配. 虚线为相应的目标边界：

在精细网格上求解波动方程：

可视化波在盒子上传播的情形：

Wolfram Research (2016)，PeriodicBoundaryCondition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html （更新于 2020 年）.

文本

Wolfram Research (2016)，PeriodicBoundaryCondition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html （更新于 2020 年）.

CMS

Wolfram 语言. 2016. "PeriodicBoundaryCondition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html.

APA

Wolfram 语言. (2016). PeriodicBoundaryCondition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html 年

BibTeX

@misc{reference.wolfram_2024_periodicboundarycondition, author="Wolfram Research", title="{PeriodicBoundaryCondition}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_periodicboundarycondition, organization={Wolfram Research}, title={PeriodicBoundaryCondition}, year={2020}, url={https://reference.wolfram.com/language/ref/PeriodicBoundaryCondition.html}, note=[Accessed: 21-November-2024 ]}