PlanckRadiationLaw
PlanckRadiationLaw[temperature,λ]
指定された温度と波長 λ についてのスペクトル放射輝度を返す.
PlanckRadiationLaw[temperature,f]
指定された温度と周波数 f についてのスペクトル放射輝度を返す.
PlanckRadiationLaw[temperature,property]
指定された温度の特性値を返す.
PlanckRadiationLaw[temperature,{λ1,λ2}]
波長範囲 λ1から λ2までの,スペクトル放射輝度の積分結果を返す.
PlanckRadiationLaw[temperature,{f1,f2}]
周波数範囲 f1から f2までの,スペクトル放射輝度の積分結果を返す.
詳細
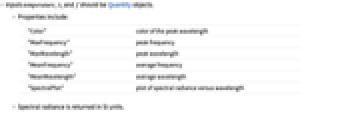
- 入力 temperature,λ,f は,Quantityオブジェクトでなければならない.
- 次は,含まれる特性である.
-
"Color" ピーク波長の色 "MaxFrequency" ピーク周波数 "MaxWavelength" ピーク波長 "MeanFrequency" 平均周波数 "MeanWavelength" 平均波長 "SpectralPlot" スペクトル放射輝度と波長のプロット - スペクトル放射輝度はSI単位で返される.
例題
すべて開くすべて閉じる例 (2)
Quantity[100,"DegreesCelsius"]におけるスペクトル放射輝度の形を調べる:
スコープ (3)
PlanckRadiationLawの全特性を見る:
アプリケーション (5)
特性と関係 (1)
PlanckRadiationLawが使う式はFormulaDataが示したものに等しい:
テキスト
Wolfram Research (2014), PlanckRadiationLaw, Wolfram言語関数, https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html (2016年に更新).
CMS
Wolfram Language. 2014. "PlanckRadiationLaw." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html.
APA
Wolfram Language. (2014). PlanckRadiationLaw. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PlanckRadiationLaw.html