WOLFRAM

Wolfram言語 ＆ システム ドキュメントセンター
Wolfram言語ホームページ »

RandomPolygon
✖
RandomPolygon

✖

n 個の頂点を持つ擬似ランダムな単純多角形を与える．

✖

指定された spec の擬似ランダムな多角形を与える．

✖
RandomPolygon[spec,k]

k 個の擬似ランダムな多角形のリストを与える．

✖
RandomPolygon[dspec,…]

次元 d の擬似ランダムな多角形を与える．

詳細とオプション

例題

すべて開くすべて閉じる

例  (3)基本的な使用例

ランダムな多角形を生成する：

In[14]:=14
✖
https://wolfram.com/xid/09b1hfm3e-gzw9nf
Out[14]=14
In[15]:=15
✖
https://wolfram.com/xid/09b1hfm3e-zbv0zl
Out[15]=15

ランダムな凸多角形のリストを生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-j5sgym
Out[1]=1

面積を計算する：

In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-sr2mfw
Out[2]=2

三次元の多角形のリストを生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-3umn6j
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-mc86oy
Out[2]=2

スコープ  (15)標準的な使用例のスコープの概要

基本的な用法  (6)

ランダムな頂点数のランダムな多角形を生成する：

In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-tkcni3
Out[2]=2

指定された頂点数のランダムな多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-ilzzic
Out[1]=1

に指定された数の頂点があるランダムな多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-042rp8
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-ewi3q5
Out[2]=2

：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-kzg04t
Out[3]=3

多角形のリストを生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-cpuziu
Out[1]=1

多角形のリストを複数生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-oj8591
Out[1]=1

指定の特性があるランダムな多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-nnond
Out[1]=1

凸多角形  (2)

ランダムな凸多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-ztst50
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-viktph
Out[2]=2

のランダムな凸多角形：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-xbys5q
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-qg6v4t
Out[2]=2

：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-8ifgd4
Out[3]=3

凸包多角形  (3)

ランダムな凸包多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-505tos
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-k3fokv
Out[2]=2

のランダムな凸包多角形：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-kjq819
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-h23e6d
Out[2]=2

：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-2hbrgv
Out[3]=3

ディリクレ(Dirichlet)分布からランダムな凸包多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-ugm62a
Out[1]=1

一様分布から：

In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-cqgw6
Out[2]=2

正規分布から：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-vdulp5
Out[3]=3

二変量正規分布から：

In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-n3lsap
Out[4]=4

単純多角形  (2)

ランダムな単純多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-nok5s6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-110gbx
Out[2]=2

のランダムな単純多角形：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-3601nb
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-z2aff1
Out[2]=2

：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-1zh9td
Out[3]=3

星形多角形  (2)

ランダムな星形多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-mv3us4
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-ud4gxz
Out[2]=2

のランダムな星形多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-jwo98e
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-lim4id
Out[2]=2

：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-1pansj
Out[3]=3

オプション  (8)各オプションの一般的な値と機能

DataRange  (1)

DataRangeを使って生成する頂点の範囲を指定することができる：

In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-ewpnb1
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/09b1hfm3e-3k5agw
Out[5]=5

別の範囲を指定する：

In[9]:=9
✖
https://wolfram.com/xid/09b1hfm3e-fl0z4t
Out[9]=9
In[10]:=10
✖
https://wolfram.com/xid/09b1hfm3e-fto0mi
Out[10]=10

WorkingPrecision  (1)

ランダムな多角形を機械演算で生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-rhun3x
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-t1z74c
Out[2]=2

30桁精度を使う：

In[5]:=5
✖
https://wolfram.com/xid/09b1hfm3e-oj80em
Out[5]=5
In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-uzay4c
Out[6]=6

VertexColors  (2)

頂点に色が付いたランダムな多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-n0f86g
Out[1]=1

3Dのランダムな多角形の頂点色を指定する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-03wv8b
Out[1]=1

VertexNormals  (1)

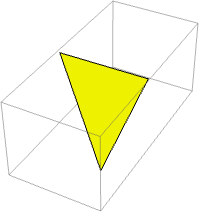
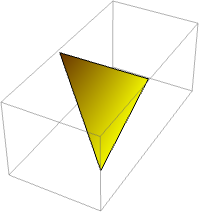
ランダムな多角形を生成する．辺ベクトルのクロス積を使って法線ベクトルを計算する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-eliva
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-lx25c
In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-bpd9f0
Out[3]=3

法線がある三角形：

In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-cvwg32
Out[4]=4

別の法線を使うと陰影付けに影響がある：

In[5]:=5
✖
https://wolfram.com/xid/09b1hfm3e-dxgk6r
Out[5]=5

VertexTextureCoordinates  (3)

2Dのランダムな多角形のテクスチャマッピング：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-1jlxp
Out[1]=1

統一されていない座標値を使ってテクスチャを繰り返す：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-drfwj5
Out[1]=1

VertexColorsはテクスチャマッピングに先行する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-ew2q5d
Out[1]=1

アプリケーション  (5)この関数で解くことのできる問題の例

基本的な用法  (2)

10個の頂点があるランダムな多角形：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-13y0bb
Out[1]=1

凸多角形：

In[2]:=2
✖
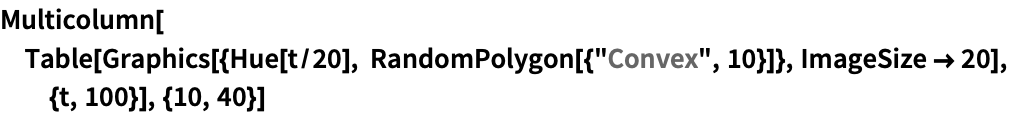
https://wolfram.com/xid/09b1hfm3e-ylmn0u
Out[2]=2

星形多角形：

In[3]:=3
✖
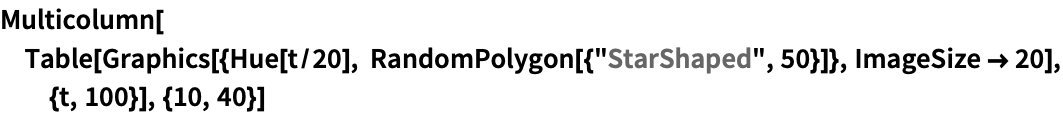
https://wolfram.com/xid/09b1hfm3e-yd2ylj
Out[3]=3

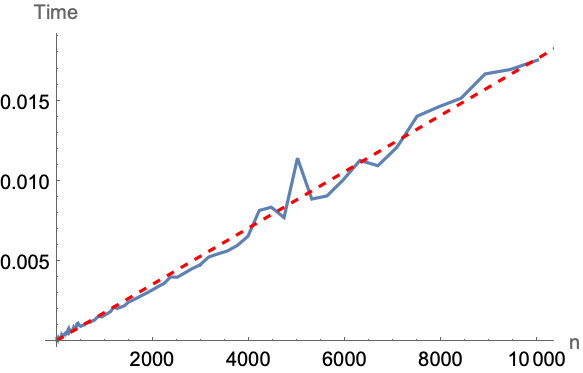
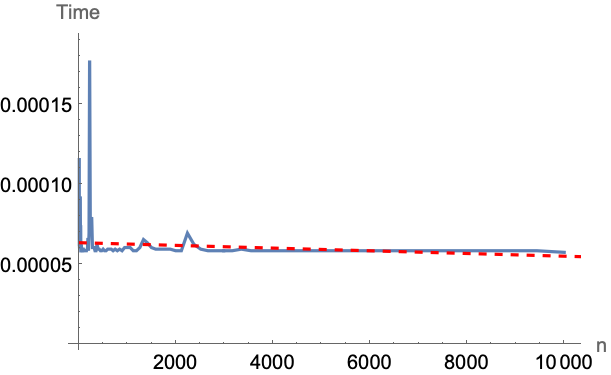
アルゴリズムのテストと計算時間の検証のためにランダムな多角形を生成する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-dko19g
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-i6opfi
In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-34otit
Out[3]=3

凸多角形のアルゴリズムの計算時間：

In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-hqm8h7
In[5]:=5
✖
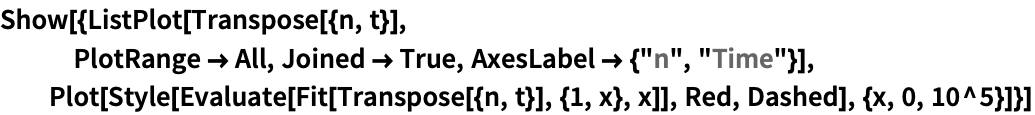
https://wolfram.com/xid/09b1hfm3e-oztoqj
Out[5]=5

単純多角形：

In[6]:=6
✖
https://wolfram.com/xid/09b1hfm3e-rfz1gt
In[7]:=7
✖
https://wolfram.com/xid/09b1hfm3e-b30lc3
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/09b1hfm3e-qj1z3e
In[9]:=9
✖
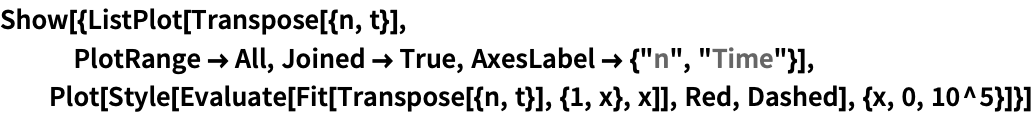
https://wolfram.com/xid/09b1hfm3e-lhrb1f
Out[9]=9

幾何学特性  (2)

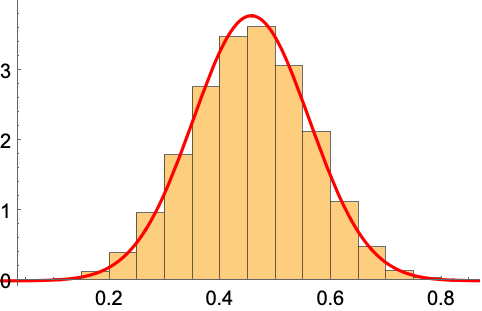
ランダムな凸多角形のシミュレーションを行い，面積を計算する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-ncrgok
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-totrtx

分布を推測する：

In[6]:=6
✖
https://wolfram.com/xid/09b1hfm3e-4wy34r
Out[6]=6

ヒストグラムとPDFを比較する：

In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-edkzjq
Out[4]=4

単位正方形上の10個の頂点がある多角形の平均面積：

In[5]:=5
✖
https://wolfram.com/xid/09b1hfm3e-ztgkxx
Out[5]=5

が に近付くとき，ランダムな凸多角形の極限の形はsqrt(1-TemplateBox[{x}, Abs])+sqrt(1-TemplateBox[{y}, Abs])=1である：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-luagb2
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-r6slzi
In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-jkelou
Out[3]=3

その他のアプリケーション  (1)

機械学習を使った多角形の分類．多角形の例で分類器関数を訓練する：

In[16]:=16
✖
https://wolfram.com/xid/09b1hfm3e-qvoctg
In[18]:=18
✖
https://wolfram.com/xid/09b1hfm3e-h9jsbn
Out[18]=18

この分類器関数を使って新たな多角形を分類する：

✖
https://wolfram.com/xid/09b1hfm3e-qw0snw
In[19]:=19
✖
https://wolfram.com/xid/09b1hfm3e-1tu3rl
Out[19]=19
In[20]:=20
✖
https://wolfram.com/xid/09b1hfm3e-wuyym3
Out[20]=20

単純多角形：

In[21]:=21
✖
https://wolfram.com/xid/09b1hfm3e-7l1pq5
Out[21]=21
In[22]:=22
✖
https://wolfram.com/xid/09b1hfm3e-h9giye
Out[22]=22

星形多角形：

In[23]:=23
✖
https://wolfram.com/xid/09b1hfm3e-rbiptp
Out[23]=23
In[24]:=24
✖
https://wolfram.com/xid/09b1hfm3e-b7ktjr
Out[24]=24

特性と関係  (5)この関数の特性および他の関数との関係

SeedRandomを使って繰り返し可能なランダムな多角形を得る：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-udvhjo
Out[1]=1
In[1]:=1
✖
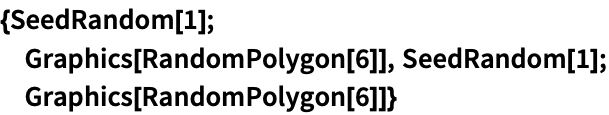
https://wolfram.com/xid/09b1hfm3e-d4tuy1
Out[1]=1

BlockRandomを使ってRandomPolygonの使用が他に影響しないようにする：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-narvr5
Out[1]=1

ConvexPolygonQを使ってランダムな多角形の特性をチェックする：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-lls03k
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-gocq6x
Out[2]=2

SimplePolygonQ：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-8ydwhn
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/09b1hfm3e-xbvx3r
Out[4]=4

ランダムな多角形のOuterPolygonは単純多角形である：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-nfp4bk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-j4pdym
Out[2]=2

ランダムな多角形には穴がない：

In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-zpe33y
Out[3]=3

PolygonDecompositionを使って多角形を凸多角形に分解する：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-49ud06
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-kq0zoo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/09b1hfm3e-nu6nus
Out[3]=3

おもしろい例題  (1)驚くような使用例や興味深い使用例

ランダムな多角形の集合：

In[1]:=1
✖
https://wolfram.com/xid/09b1hfm3e-w5cml6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/09b1hfm3e-5tdpmu
Out[2]=2
Wolfram Research (2019), RandomPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPolygon.html.
✖
Wolfram Research (2019), RandomPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPolygon.html.

テキスト

Wolfram Research (2019), RandomPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPolygon.html.

✖
Wolfram Research (2019), RandomPolygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/RandomPolygon.html.

CMS

Wolfram Language. 2019. "RandomPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPolygon.html.

✖
Wolfram Language. 2019. "RandomPolygon." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPolygon.html.

APA

Wolfram Language. (2019). RandomPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPolygon.html

✖
Wolfram Language. (2019). RandomPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPolygon.html

BibTeX

@misc{reference.wolfram_2025_randompolygon, author="Wolfram Research", title="{RandomPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPolygon.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_randompolygon, author="Wolfram Research", title="{RandomPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPolygon.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_randompolygon, organization={Wolfram Research}, title={RandomPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/RandomPolygon.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_randompolygon, organization={Wolfram Research}, title={RandomPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/RandomPolygon.html}, note=[Accessed: 04-April-2025 ]}