RegionDifference

RegionDifference[reg1,reg2]

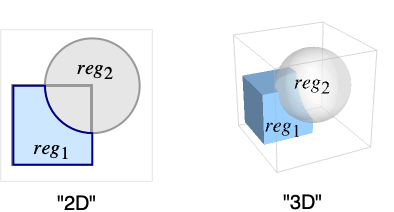
gives the difference of the regions reg1 and reg2.

Details and Options

Examples

open allclose all

Basic Examples  (2)

Difference of two disks:

Visualize it:

Difference of two MeshRegion objects:

Scope  (12)

Special Regions  (6)

For some regions, the difference is computed explicitly:

The regions are disjoint:

Here the difference is empty:

The cuboid is contained in the ball:

A difference of Line regions:

Visualize it:

A difference of Polygon regions:

Visualize it:

A difference of two Cuboid regions:

Visualize it:

A difference of regions with different RegionDimension:

Visualize it:

Formula Regions  (2)

A difference of ImplicitRegion objects is an ImplicitRegion:

2D:

3D:

nD:

A difference of ParametricRegion objects:

Visualize it:

Mesh Regions  (2)

A difference of BoundaryMeshRegion objects is a BoundaryMeshRegion:

2D:

3D:

A difference of full-dimensional MeshRegion objects is a MeshRegion:

2D:

3D:

Derived Regions  (2)

A difference of BooleanRegion objects:

Visualize it:

A difference of TransformedRegion objects:

Visualize it:

Applications  (4)

Difference of regions:

Define a disk annulus as the difference of two disks:

The area is the difference of areas:

Define a ball shell (sometimes called spherical shell) as the generalization of an annulus to 3D:

The volume is the difference of volumes:

Create illusory contours:

Properties & Relations  (5)

A point p belongs to RegionDifference[reg1,reg2] if it belongs to reg1 but not reg2:

Use RegionMember to test membership:

RegionDifference is a Boolean combination ¬#2∧#1 of two regions:

RegionSymmetricDifference can be found using RegionUnion and RegionDifference:

The RegionDimension of a difference is at most that of the first input:

It can be less, however:

This difference is a line segment, and thus has dimension 1:

If two regions are disjoint, the RegionMeasure of their difference is that of the first input:

If they overlap, you must subtract the measure of the RegionIntersection:

Possible Issues  (1)

Difference is defined only for regions with the same RegionEmbeddingDimension:

Neat Examples  (1)

The difference of two spiral polygons:

Wolfram Research (2014), RegionDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDifference.html (updated 2017).

Text

Wolfram Research (2014), RegionDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDifference.html (updated 2017).

CMS

Wolfram Language. 2014. "RegionDifference." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RegionDifference.html.

APA

Wolfram Language. (2014). RegionDifference. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDifference.html

BibTeX

@misc{reference.wolfram_2024_regiondifference, author="Wolfram Research", title="{RegionDifference}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionDifference.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regiondifference, organization={Wolfram Research}, title={RegionDifference}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionDifference.html}, note=[Accessed: 21-November-2024 ]}