RegionMoment

RegionMoment[reg,{i1,i2,…,in}]

領域 reg についての多項式モーメント を計算する．

詳細とオプション

例題

すべて開くすべて閉じる

例  (2)

球体上で多項式モーメント を求める：

その領域でパラメータのあるモーメントを求める：

さまざまなベキ乗のモーメントを求める：

スコープ  (10)

特別な領域  (1)

さまざまな特別領域のモーメントをさまざまな次元で求める：

数式定義領域  (2)

ImplicitRegionとして表された円板のモーメント：

円柱のモーメント：

ParametricRegionとして表された円板のモーメント：

円板の有理パラメータ化を使用する：

円柱を求める：

メッシュ領域  (2)

2DのMeshRegionのモーメント：

3Dの：

BoundaryMeshRegionのモーメント：

3Dの：

派生領域  (3)

RegionIntersectionのモーメント：

TransformedRegionのモーメント：

RegionBoundaryのモーメント：

地理的領域  (2)

GeoPositionを使った多角形のモーメント：

GeoGridPositionを使った多角形のモーメント：

アプリケーション  (3)

零次RegionMomentを使って牛の表面積を求める：

各軸について一次モーメントを使ってその重心を求める：

RegionMeasureとRegionCentroidを使って結果を確かめる：

領域で定義された定密度分布の共分散行列を求める：

RegionCentroidが原点となるように領域を変換する：

二次モーメントの行列を計算し，RegionMeasureで割ることでそれを正規化する：

牛の表面と最初の4つのモーメントを共有する曲面を求める：

この曲面は牛と同じ表面積と重心を持つ：

特性と関係  (8)

曲線の零次モーメントはArcLengthに等しい：

曲面の零次モーメントはAreaに等しい：

立体の零次モーメントはVolumeに等しい：

任意の領域の零次モーメントはRegionMeasureに等しい：

RegionCentroidは一次モーメントを零次モーメントで割ったものである：

重心はで与えられる：

重心と比較する：

MomentOfInertiaは複数の領域モーメントからなる原点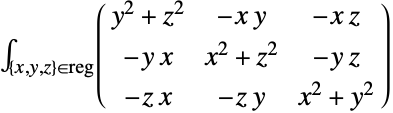についての回転慣性行列を計算する：

MomentはPDF についての を計算する：

RegionMomentは一様密度に相当する を計算する：

CentralMomentはPDF と重心 についての を計算する：

領域を中心化した後では，これは標準モーメントになる：

前の例のように，RegionMomentは一様分布を仮定する：

Wolfram Research (2016), RegionMoment, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMoment.html.

テキスト

Wolfram Research (2016), RegionMoment, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionMoment.html.

CMS

Wolfram Language. 2016. "RegionMoment." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionMoment.html.

APA

Wolfram Language. (2016). RegionMoment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionMoment.html

BibTeX

@misc{reference.wolfram_2024_regionmoment, author="Wolfram Research", title="{RegionMoment}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/RegionMoment.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionmoment, organization={Wolfram Research}, title={RegionMoment}, year={2016}, url={https://reference.wolfram.com/language/ref/RegionMoment.html}, note=[Accessed: 21-November-2024 ]}