RegionSymmetricDifference

RegionSymmetricDifference[reg1,reg2,…]

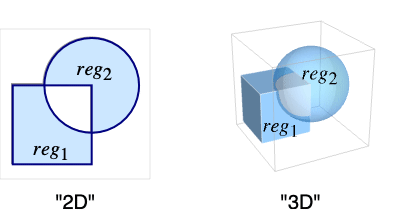
領域 reg1，reg2，…の対称差を表す．

詳細とオプション

例題

すべて開くすべて閉じる

例  (2)

2つの円板の対称差：

可視化する：

2つのMeshRegionオブジェクトの対称差：

スコープ  (10)

特別な領域  (4)

Line領域の対称差：

可視化する：

Polygon領域の対称差：

これを可視化する：

2つのCuboid領域の対称差：

RegionDimensionが異なる領域の対称差：

可視化する：

数式定義領域  (2)

ImplicitRegionオブジェクトの対称差はImplicitRegionである：

2D：

3D：

nD：

ParametricRegionオブジェクトの対称差：

可視化する：

メッシュ領域  (2)

BoundaryMeshRegionオブジェクトの対称差はBoundaryMeshRegionである：

2D：

3D：

全次元のMeshRegionオブジェクトの対称差はMeshRegionである：

2D：

3D：

派生領域  (2)

BooleanRegionオブジェクトの対称差：

可視化する：

TransformedRegionオブジェクトの対称差：

可視化する：

アプリケーション  (1)

領域の対称差：

特性と関係  (5)

点 p が奇数の regiに属するなら，その点はRegionSymmetricDifference[reg1,reg2]に属する：

RegionMemberを使って帰属判定する：

RegionSymmetricDifferenceは，領域の論理結合Xorである：

RegionSymmetricDifferenceは，RegionUnionとRegionDifferenceを使って求めることができる：

対称差のRegionDimensionは，最大で入力次元の最大のものである：

それより小さくなることもある：

この対称差は2本の線であり，したがって次元は1である：

対称差のRegionMeasureは単純な式に従う：

入力測度の総和から共通部分の測度を2回引くだけでよい：

考えられる問題  (1)

対称差はRegionEmbeddingDimensionが等しい領域についてしか定義されない：

おもしろい例題  (1)

2つの螺線多角形の対称差：

Wolfram Research (2014), RegionSymmetricDifference, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html （2017年に更新）.

テキスト

Wolfram Research (2014), RegionSymmetricDifference, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html （2017年に更新）.

CMS

Wolfram Language. 2014. "RegionSymmetricDifference." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html.

APA

Wolfram Language. (2014). RegionSymmetricDifference. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html

BibTeX

@misc{reference.wolfram_2024_regionsymmetricdifference, author="Wolfram Research", title="{RegionSymmetricDifference}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionsymmetricdifference, organization={Wolfram Research}, title={RegionSymmetricDifference}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html}, note=[Accessed: 21-November-2024 ]}