SchrodingerPDEComponent[vars,pars]
yields a Schrödinger PDE term with model variables vars and model parameters pars.


SchrodingerPDEComponent
SchrodingerPDEComponent[vars,pars]
yields a Schrödinger PDE term with model variables vars and model parameters pars.
Details



- Generates the Schrödinger equation to be used for eigensystems and time-dependent analysis. Given the variables and parameters, a PDE operator is returned.
- SchrodingerPDEComponent is the non-relativistic quantum mechanics analogous to Newton's second law and describes the time evolution of a wavefunction in quantum mechanics.
- SchrodingerPDEComponent returns a sum of differential operators to be used as a part of partial differential equations:
- SchrodingerPDEComponent can be used to model Schrödinger equations with independent variables
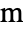 in units of meter
in units of meter ![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SchrodingerPDEComponent.en/4.png) , dependent variable
, dependent variable 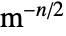 in units of
in units of ![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2) TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]^(-n/2)](Files/SchrodingerPDEComponent.en/6.png) and time variable
and time variable 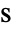 in units of
in units of ![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/SchrodingerPDEComponent.en/8.png) .
. - Stationary model variables vars are vars={Ψ[x1,…,xn],{x1,…,xn}}.
- Time-dependent model variables vars are vars={Ψ[t,x1,…,xn],t,{x1,…,xn}}.
- The SchrodingerPDEComponent is based on a kinetic term and a potential term:
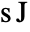 is the reduced Planck constant in units of
is the reduced Planck constant in units of ![TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "J"}, second joules, {"Joules", , "Seconds"}}, QuantityTF]](Files/SchrodingerPDEComponent.en/11.png) , and
, and 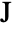 is the Schrödinger potential in units of
is the Schrödinger potential in units of ![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.en/13.png) .
.- The mass
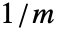 can be isotropic, orthotropic or anisotropic.
can be isotropic, orthotropic or anisotropic. 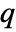 represents a
represents a 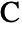 by
by 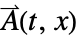 matrix given by:
matrix given by: - For a magnetic field interaction, the SchrodingerPDEComponent is:
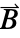 represents the electric charge of the particle in units of coulombs
represents the electric charge of the particle in units of coulombs ![TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "C", coulombs, "Coulombs"}, QuantityTF]](Files/SchrodingerPDEComponent.en/21.png) .
.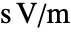 is the magnetic vector potential in units of
is the magnetic vector potential in units of ![TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "V", , "/", , "m"}, second volts per meter, {{(, {"Volts", , "Seconds"}, )}, /, {(, "Meters", )}}}, QuantityTF]](Files/SchrodingerPDEComponent.en/23.png) , defined such that
, defined such that 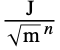 , where
, where 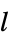 is the magnetic flux density in units of
is the magnetic flux density in units of ![TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "T", teslas, "Teslas"}, QuantityTF]](Files/SchrodingerPDEComponent.en/26.png) .
.- The units of the Schrödinger PDE terms are joules
![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]](Files/SchrodingerPDEComponent.en/27.png) times the units of the wavefunction in
times the units of the wavefunction in ![TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n TemplateBox[{InterpretationBox[, 1], "J", joules, "Joules"}, QuantityTF]/TemplateBox[{InterpretationBox[, 1], {{sqrt(, "m", )}}, square root meters, {sqrt(, "Meters", )}}, QuantityTF]^n](Files/SchrodingerPDEComponent.en/28.png) .
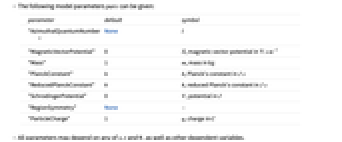
. - The following model parameters pars can be given:
-
parameter default symbol "AzimuthalQuantumNumber" None 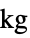
"MagneticVectorPotential" 0 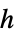 , magnetic vector potential in
, magnetic vector potential in 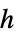
"Mass" 1 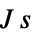 , mass in
, mass in 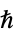
"PlanckConstant" 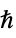
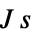 , Planck's constant in
, Planck's constant in 
"ReducedPlanckConstant" 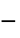
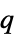 , reduced Planck's constant in
, reduced Planck's constant in 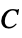
"SchrodingerPotential" 0 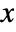
"RegionSymmetry" None 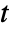
"ParticleCharge" 1 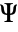 , charge in
, charge in 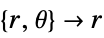
- All parameters may depend on any of
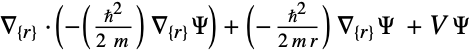 ,
, 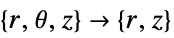 and
and 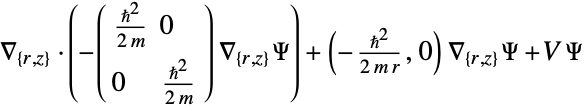 , as well as other dependent variables.
, as well as other dependent variables. - Parameters given with units are converted to SI base units.
- Default values for Planck's and reduced Planck's constants are in SI base units.
- A possible choice for the parameter "RegionSymmetry" is "Axisymmetric".
- "Axisymmetric" region symmetry represents a truncated cylindrical coordinate system where the cylindrical coordinates are reduced by removing the angle variable as follows:
-
dimension reduction general equation 1D 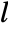
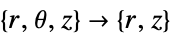
2D 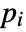
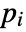
- If "RegionSymmetry" is set to "Axisymmetric",
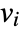 has to be isotropic.
has to be isotropic. - With an "AzimuthalQuantumNumber"
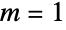 , the SchrodingerPDEComponent is:
, the SchrodingerPDEComponent is: - The diffusion component affects the meaning of NeumannValue.
- If the SchrodingerPDEComponent depends on parameters
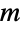 that are specified in the association pars as …,keypi…,pivi,…, the parameters
that are specified in the association pars as …,keypi…,pivi,…, the parameters 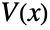 are replaced with
are replaced with 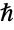 .
.
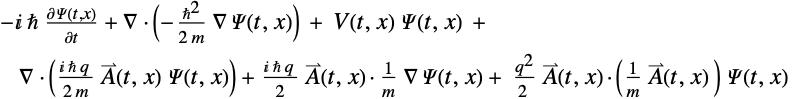
Examples
open all close allBasic Examples (3)
Specify a PDE operator for a particle with mass ![]() and potential
and potential ![]() :
:
The exact value is used for Planck's constant:
Specify a PDE operator for a particle with mass ![]() and potential
and potential ![]() with a reduced Planck constant
with a reduced Planck constant ![]() :
:
Define a Hamiltonian with a reduced Planck constant of ![]() , a harmonic potential
, a harmonic potential ![]() and a mass of
and a mass of ![]() :
:
Find the 10 smallest eigenvalues and eigenfunctions on a refined mesh:
Visualize the eigenfunctions scaled by the reduced Planck constant and offset by the respective eigenvalue:
Scope (16)
1D (6)
Define a Schrödinger PDE operator:
Define a Schrödinger PDE operator with ![]() as the Planck constant:
as the Planck constant:
Define a Schrödinger PDE operator with ![]() as the reduced Planck constant:
as the reduced Planck constant:
Define a Schrödinger PDE operator with mass ![]() :
:
Define a Schrödinger PDE operator with a potential ![]() :
:
Define a Schrödinger PDE operator with ![]() as the reduced Planck constant, mass
as the reduced Planck constant, mass ![]() , a magnetic vector potential
, a magnetic vector potential ![]() and charge
and charge ![]() :
:
2D (1)
3D (2)
Axisymmetric (3)
Specify an axisymmetric time-independent Schrödinger PDE term with the reduction ![]() , for a particle with mass
, for a particle with mass ![]() , reduced Planck constant
, reduced Planck constant ![]() and a potential
and a potential ![]() :
:
Specify an axisymmetric time-independent Schrödinger PDE term with the reduction ![]() , for a particle with mass
, for a particle with mass ![]() , reduced Planck constant
, reduced Planck constant ![]() and a potential
and a potential ![]() :
:
Define a PDE operator with a reduced Planck constant ![]() , a mass
, a mass ![]() and an azimuthal quantum number
and an azimuthal quantum number ![]() :
:
Time-Dependent (1)
Applications (12)
Compute the eigensystem of a time-independent Schrödinger PDE operator with a Planck constant of 1, a mass of 1 and a potential ![]() :
:
Visualize the eigenfunctions and label the eigenvalues:
Find the 10 smallest eigenvalues and eigenfunctions with a reduced Planck constant ![]() and a piecewise potential that is
and a piecewise potential that is ![]() for negative values of
for negative values of ![]() and
and ![]() for positive values of
for positive values of ![]() .
.
Find the 10 smallest eigenvalues and eigenfunctions on a refined mesh:
Look at the energy eigenvalues:
Visualize the eigenfunctions scaled by ![]() and offset by the respective eigenvalue:
and offset by the respective eigenvalue:
Describe a particle confined in a two-dimensional disk of radius ![]() , assuming symmetry around the axis that passes through the center of the disk. Assume that the wavefunction for the particle has no polar coordinate dependence.
, assuming symmetry around the axis that passes through the center of the disk. Assume that the wavefunction for the particle has no polar coordinate dependence.
Set up an axisymmetric Schrödinger PDE operator, with a Planck constant equal to ![]() :
:
The potential energy outside the region is infinite, then the wavefunction vanishes at the boundary.
Define a Dirichlet boundary condition:
Visualize the probabiity densities:
Consider a model in which the wavefunction can be separated in the following way: ![]() , where
, where ![]() ,
, ![]() and
and ![]() are the radial, azimuthal and height coordinates in a cylindrical coordinate system, respectively. Here,
are the radial, azimuthal and height coordinates in a cylindrical coordinate system, respectively. Here, ![]() is the azimuthal quantum number.
is the azimuthal quantum number.
This particular example considers a particle confined in a torus with infinite potential walls. Given these considerations, it is only necessary to solve for ![]() in a cross section of the torus.
in a cross section of the torus.
Define the major radius of the torus:
Define the region with a minor radius of ![]() :
:
Visualize the mesh as the torus cross section it represents:
Define the boundary condition such that the wavefunction vanishes at the boundary of the torus:
Create a helper function to find six eigenstates for different values of the azimuthal quantum number with a PDE operator such that ![]() and
and ![]() for a simplified model and
for a simplified model and ![]() for the particle inside the torus:
for the particle inside the torus:
It is possible to explore how the energy levels vary for different values of the azimuthal quantum number. To exemplify this, calculate the energy for ![]() between 0 and 5.
between 0 and 5.
Calculate the energy eigenvalues for each value of ![]() between 0 and 5:
between 0 and 5:
Plot the energy eigenvalues as a function of the azimuthal quantum number:
Observe how the energy levels grow nonlinearly as ![]() grows. Also, it can be noticed how the ground state is non-degenerate, while states two and three, as well as four and five, are two-fold degenerate.
grows. Also, it can be noticed how the ground state is non-degenerate, while states two and three, as well as four and five, are two-fold degenerate.
To explore the effect of the azimuthal quantum number on the wavefunctions, plot the real and imaginary parts of the total wavefunction ![]() . For this purpose, you can choose any value of
. For this purpose, you can choose any value of ![]() , for instance,
, for instance, ![]() .
.
Calculate the energy and the part of the wavefunction that depends on ![]() and
and ![]() :
:
Plot the real and imaginary parts of the wavefunction ![]() :
:
Now plot the probability densities for the same value of ![]() :
:
The probability density is independent of the coordinate ![]() , as expected.
, as expected.
You can study a quantum billiard system, in particular, a particle confined in a 2D Bunimovich stadium.
Define the region and visualize it:
Generate a Schrödinger operator with no potential:
Given that the potential energy outside the region is infinite, the wavefunction vanishes at the boundary.
Define the boundary condition:
Find the first 100 eigenstates:
Plot the wavefunctions for different states:
Set up a time-dependent Schrödinger PDE operator with a reduced Planck constant:
Solve the equation with a Gaussian as an initial setting:
Apply Animate to the solution:
Set up a nonlinear, time-dependent Schrödinger PDE operator:
Define boundary and initial conditions:
Plot the absolute value of the solution:
Set up a time-dependent Schrödinger PDE operator with a harmonic potential:
Solve the equation with a coherent state as an initial setting:
Animate the probability density with the potential scaled down by a factor of ![]() :
:
Set up a time-dependent Schrödinger PDE operator with a reduced Planck constant and a Gaussian potential ![]() :
:
Specify an initial condition of a wave packet with positive momentum:
Visualize it along with the potential that is being scaled down by a ![]() factor to fit in the plot:
factor to fit in the plot:
Solve the equation with a refined mesh:
Visualize the solution where the vertical and horizontal axes represent time, ![]() , and position,
, and position, ![]() , respectively:
, respectively:
Note that at about ![]() , the wave packed hits the wall and gets reflected.
, the wave packed hits the wall and gets reflected.
Visualize the solution with an animation:
Define an operator for a free particle:
Define a region that defines the double slit and visualize it:
Set up the initial conditions as a wave packet:
Visualize the initial condition:
You can model a spinless charged particle in a magnetic field that is pointing in the ![]() direction. The particle is described by an initial wave packet, and the goal is to study the evolution of the probability density under magnetic field interaction. Since this is a charged particle in a magnetic field, one can expect for its probability density to reflect some kind of circular trajectory, similar to the behavior of classical charged particles. For that reason, a very high magnetic flux density has been chosen, such that the cyclotron radius is in the order of angstroms.
direction. The particle is described by an initial wave packet, and the goal is to study the evolution of the probability density under magnetic field interaction. Since this is a charged particle in a magnetic field, one can expect for its probability density to reflect some kind of circular trajectory, similar to the behavior of classical charged particles. For that reason, a very high magnetic flux density has been chosen, such that the cyclotron radius is in the order of angstroms.
Set up the reduced Planck constant, particle's mass, magnetic flux density and the particle's electric charge, respectively:
Define a constant ![]() to measure the time in femtoseconds:
to measure the time in femtoseconds:
The particle's initial condition will be described by a wave packet with a momentum ![]() , meaning it would move in a straight line if there were no magnetic field interaction.
, meaning it would move in a straight line if there were no magnetic field interaction.
A magnetic flux density is chosen to have a cyclotron radius in the order of angstroms.
Compute the cyclotron radius of the particle:
The magnetic vector potential can be chosen such that ![]() :
:
The work region can be defined as a rectangle of ![]()
![]() .
.
Since the length units are Angstroms (![]() ), you need to take that into account when defining the PDE operator. For that reason, "ScaleUnits" -> {"Meters" -> "Angstroms"} are used in the parameters argument of the SchrodingerPDEComponent.
), you need to take that into account when defining the PDE operator. For that reason, "ScaleUnits" -> {"Meters" -> "Angstroms"} are used in the parameters argument of the SchrodingerPDEComponent.
Define a Schrödinger PDE operator that assumes Coulomb's gauge for the magnetic vector potential:
Change the units of ![]() to be used in the boundary condition:
to be used in the boundary condition:
Solve the problem with a transparent boundary condition with a NeumannValue:
As a demonstration of the Aharonov–Bohm effect, the scattering process of a wave packet that is passing through two slits under the influence of a magnetic vector potential is modeled. Notice that the magnetic flux density is zero for the entire solving domain, but the magnetic vector potential is not.
For instance, a domain is defined with two slits and a small hole that represents a long solenoid producing a magnetic flux density inside it, and in turn, producing a magnetic vector potential field throughout the rest of the domain. Note that the wavefunction cannot interact with a region in which the magnetic flux density is nonzero.
Define variables and parameters such that the mass is non-isotropic, with values of the effective masses of heavy holes in ![]() , a common semiconductor material. Here, the "MagneticVectorPotential" parameter is for a solenoid with a magnetic flux density of
, a common semiconductor material. Here, the "MagneticVectorPotential" parameter is for a solenoid with a magnetic flux density of ![]() and a radius of
and a radius of ![]() , transformed into Cartesian coordinates.
, transformed into Cartesian coordinates.
Define variables and parameters:
Animate the evolution of the probability density:
Notice how the interference pattern is shifted compared with the case of no magnetic field, and is non-symmetric.
Properties & Relations (3)
Specify an operator for a particle with mass ![]() and potential
and potential ![]() with a reduced Planck constant
with a reduced Planck constant ![]() :
:
When parameters are given with units, they are automatically converted to SI base units.
Specify a PDE operator with the electron's mass and the reduced Planck constant ![]() :
:
Inspect the difference between each unit system in the diffusion coefficient. Compute the Planck constant divided by the electron mass:
Convert the result to SI base units:
This example shows that at an internal interface, the BenDaniel–Duke boundary conditions are applied automatically.
Consider a quantum well with width ![]() , a finite potential
, a finite potential ![]() and wavefunction
and wavefunction ![]() . The particle's mass within the well is
. The particle's mass within the well is ![]() , while the particle's mass in the barrier region is
, while the particle's mass in the barrier region is ![]() . The mass thus is a function of the position
. The mass thus is a function of the position ![]() . The quantities
. The quantities ![]() and
and ![]() , should be continuous at interfaces between the barrier and the well region, and the BenDaniel–Duke boundary conditions should be applied at the interface. In fact, the BenDaniel–Duke boundary conditions are applied automatically at the interface.
, should be continuous at interfaces between the barrier and the well region, and the BenDaniel–Duke boundary conditions should be applied at the interface. In fact, the BenDaniel–Duke boundary conditions are applied automatically at the interface.
Note that the domain's length unit of the well, ![]() is in angstroms. To define the PDE operator, the parameter "ScaleUnits"->{"Meters"->"Angstroms"} is used. This converts the rest of the model quantities such that all length units are now in angstroms. This improves the quality of the numerical solution.
is in angstroms. To define the PDE operator, the parameter "ScaleUnits"->{"Meters"->"Angstroms"} is used. This converts the rest of the model quantities such that all length units are now in angstroms. This improves the quality of the numerical solution.
Physically, the wavefunction should decay until it goes to ![]() for all bound states at infinity. A practical modeling approach is to use a Dirichlet boundary condition with
for all bound states at infinity. A practical modeling approach is to use a Dirichlet boundary condition with ![]() at the external boundary, which is heuristically chosen to be placed at a long enough distance from the center of the quantum well. In this case, a distance of
at the external boundary, which is heuristically chosen to be placed at a long enough distance from the center of the quantum well. In this case, a distance of ![]() works well for this purpose.
works well for this purpose.
Define the Dirichlet condition:
Solve the eigenvalue problem with NDEigensystem on a refined mesh:
The units of the eigenvalues are ![]() , given that the meters units were scaled in the parameters to angstroms. Knowing this,the eigenvalues can then be transformed to the desired energy unit.
, given that the meters units were scaled in the parameters to angstroms. Knowing this,the eigenvalues can then be transformed to the desired energy unit.
Redefine the energy eigenvalues with the correct units:
Finally, the energy eigenvalues and probability densities can be compared between the numerical and analytical approaches.
Define the code for the analytical eigenvalues:
Define the analytic wavefunctions code:
Plot the numerical and analytical probability densities together:
Compare the difference between the analytical solution and the numerical one:
The above has shown that the energy eigenvalues provided by NDEigensystem are numerically the same as the analytical solution to the Schrödinger equation when BenDaniel–Duke boundary conditions are implemented. Furthermore, the wavefunctions obtained by NDEigensystem are equivalent to the analytical solution. This is the case because the numerical procedure ensures the continuity of both the wavefunction ![]() and the quantity
and the quantity ![]() .
.
Neat Examples (1)
Define a quantum well potential energy as a piecewise function:
Set up the variables and parameters, with the mass and the reduced Planck constant equal to ![]() , for a simplified Schrödinger PDE operator:
, for a simplified Schrödinger PDE operator:
Use NDEigensystem to solve the time-independent Schrödinger equation in one dimension. The objective of this visualization is to see the effect that the barrier height and the well's length have on the eigenstates. One can see how increasing the well's length decreases the energy for each wavefunction. On the other hand, increasing the barrier height results in higher energy eigenvalues.
Define a function to calculate the eigenstates for any given value of potential barrier, well's width or number of eigenstates:
Set up a Manipulate:
Tech Notes
Related Guides
Text
Wolfram Research (2024), SchrodingerPDEComponent, Wolfram Language function, https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html (updated 2024).
CMS
Wolfram Language. 2024. "SchrodingerPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html.
APA
Wolfram Language. (2024). SchrodingerPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_schrodingerpdecomponent, author="Wolfram Research", title="{SchrodingerPDEComponent}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html}", note=[Accessed: 26-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_schrodingerpdecomponent, organization={Wolfram Research}, title={SchrodingerPDEComponent}, year={2024}, url={https://reference.wolfram.com/language/ref/SchrodingerPDEComponent.html}, note=[Accessed: 26-January-2026]}