Sign

Sign[x]

x が負，ゼロ，正のときに，それぞれ-1，0，1を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • Sign[z]は，ゼロではない複素数 z については z/Abs[z]として定義される．
  • Signは，シンボル式の符号を判定するために，さまざまな変換を試みる．
  • 厳密な数値に対して，Signは内部で数値近似を使い結果を見出す．この過程は大域的変数$MaxExtraPrecisionの設定によって影響を受ける．
  • Signは自動的にリストに縫い込まれる． »
  • SignはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (4)

実数：

複素数：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

スコープ  (32)

数値評価  (6)

数値的に評価する：

複素数入力：

高精度で評価する：

実数の入力についての結果は厳密値になる：

複素数の入力については，出力精度は入力精度に従う：

高精度で効率的に評価する：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のSign関数を計算することもできる：

SignはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる：

Aroundを使って平均的な場合の統計区間を計算することもできる：

特定の値  (5)

固定点におけるSignの値：

ゼロにおける値：

無限大における値：

記号的に評価する：

TemplateBox[{x}, Sign]=0となるような の値を求める：

結果を可視化する：

可視化  (4)

TemplateBox[{{x, +, 1}}, Sign]を実軸上でプロットする：

関数の実部と虚部をプロットする：

Signを三次元で可視化する：

関数の実部をプロットする：

関数の虚部をプロットする：

関数の特性  (12)

Signはすべての実数値と複素数値の入力について定義される：

実数値入力についてのSign関数の値域：

複素平面上の値域は単位円に原点を加えたものである：

Signは奇関数である：

Signは鏡特性 TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox]}, Sign]=TemplateBox[{TemplateBox[{z}, Sign]}, Conjugate]を持つ：

Signは微分可能な関数ではない：

差分商は複素平面上に極限を持たない：

特定の方向（例えば実数方向）にだけ唯一の極限がある：

RealSignを使って実数の微分可能な結果を得る：

Signは解析関数ではない：

特異点と不連続点の両方を持つ：

複素平面上では，あらゆるところに特異点を持つが，不連続になるのは原点だけである：

Signは非増加である：

Signは単射ではない：

Signは全射ではない：

Signは非負でも非正でもない：

Signは凸でも凹でもない：

TraditionalFormによる表示：

関数の恒等式と簡約  (5)

実変数 x と y を仮定して展開する：

適切な仮定を使ってSignを簡約する：

複素数をSignとAbsの積として表す：

は に等しい：

すべての非零の についてTemplateBox[{TemplateBox[{z}, Sign]}, Abs]=1である：

アプリケーション  (2)

Signの実部と虚部を複素平面上でプロットする：

Rademacher関数を定義する：

Rademacher関数を（垂直方向にシフトして）プロットする：

単位区間で直交性をチェックする：

特性と関係  (10)

単純な引数のSignは自動的に，より簡単な形に評価される：

Signはベキ等元である：

FullSimplifyを使ってSignを含む式を簡約する：

付加的な仮定を用いて簡約する：

実変数を仮定する：

SignをComplexExpandの目的関数として用いる：

Signを定積分で使う：

複素平面上の線に沿って記号的かつ数値的に積分する：

複素数値については，不定積分は経路依存である：

実数値についての不定積分：

積分変換に用いる：

積分と極限からSignを得る：

Piecewiseに変換する：

ネストを外す：

考えられる問題  (5)

Signは複素変数関数なので微分不可能である：

Sign[z]は複素関数なので，Conjugate[z]なしで書くことはできない：

特に，導関数を定義する極限は方向に依存するので存在しない：

引数は実数であると仮定するRealSignを使ってSignの微分可能なバージョンを得る：

純粋に実数のあるいは虚数の近似引数の場合，Signは厳密な答を返す：

一般的な複素引数についてはSignは入力精度を引き継ぐ：

数値引数については，Signが未評価のままになることがある：

Signを機械精度で数値的に評価すると，正しくない答が返されることがある：

任意精度の評価は正しい結果を返す：

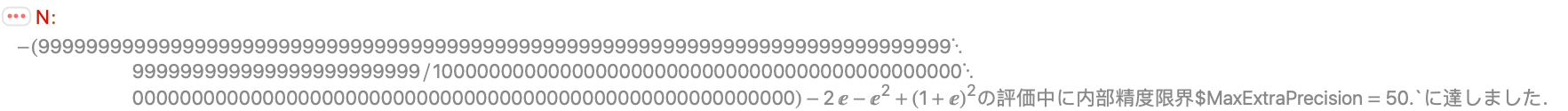
$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

行列に適用されたSignは行列符号関数を返さない：

おもしろい例題  (3)

3つの符号関数の対称積から始めて繰り返されるたたみ込み積分を形成する：

一般化されたフーリエ級数を通してSignを近似する：

Signの有理近似を計算する：

Wolfram Research (1988), Sign, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sign.html （2021年に更新）.

テキスト

Wolfram Research (1988), Sign, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sign.html （2021年に更新）.

CMS

Wolfram Language. 1988. "Sign." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Sign.html.

APA

Wolfram Language. (1988). Sign. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sign.html

BibTeX

@misc{reference.wolfram_2024_sign, author="Wolfram Research", title="{Sign}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Sign.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sign, organization={Wolfram Research}, title={Sign}, year={2021}, url={https://reference.wolfram.com/language/ref/Sign.html}, note=[Accessed: 21-November-2024 ]}